座標で解こう

どうも、フジです。

前回の記事で「座標で解く」暇つぶし数学を紹介しました。せっかくなので、それの実践編。今回は京都大学の問題を座標で解いてみようかなと思います。

京大数学を解こう

これは1998年の京大文系数学第2問の問題です。パッと見、三角比を使って解くのかなあという雰囲気を感じますが、座標で解きます。今回はそういう縛りプレイです。

まずは”一辺の長さが1の正四面体OABC”を座標空間上に落とし込みます。長さが1の正四面体ということで、立体図形の形自体は変化しない、ありがたいタイプ。非常にプロットしやすいですね。前回の記事で書いた通り、原点を利用しつつ、対称性を考慮しながら、どう配置するかを考えます。加えて、今回ポイントとなってくるのは「点Pが動き、そして線分BPの長さがxである」という部分。このxが、そのまま座標になるように配置したいなあという気持ちになりますね。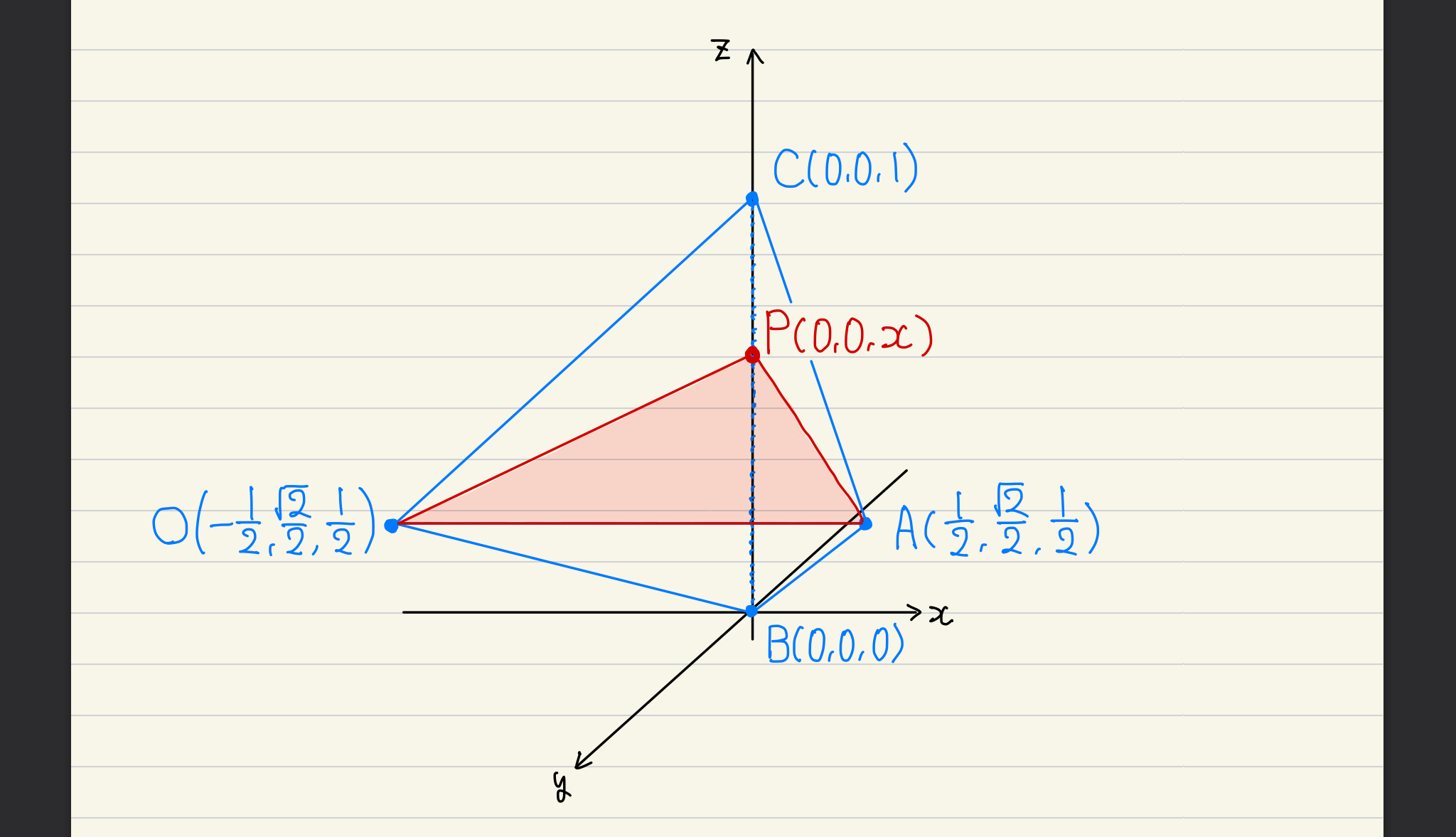



ということで、私はこんな感じに落とし込みました。今回は三角形OAPの面積を追いかけるわけですが、こう見るとめちゃくちゃわかりやすいと思いません？ 座標に落とし込むと、図形をより捉えやすくなるんですよね。

じゃあここからは、実際に三角形の面積を求めていこうかなと思います。ちなみに、三角形の面積の求め方って4通りあるんですけど、パッと言えますか？

初等幾何/座標/三角比/ベクトルの4通り。きちんと使い分けられるようにしてくださいね。今回は初等幾何、つまり底辺×高さ÷2で攻めるのが楽かなと思います。辺ABを三角形OAPの底辺と捉えると、線分ABの中点(以下点Mとする)と点Pの間の距離がちょうど高さとなる。要するに線分MPの長さをxを用いて表すことさえできれば勝ちってこと。この時点で、ゴールまでの道筋がザックリ思い描けます。

「立体図形は切断して平面で捉える」というのが原則。以下のように切断すれば、線分MPの長さは、三平方の定理で求めることが可能です。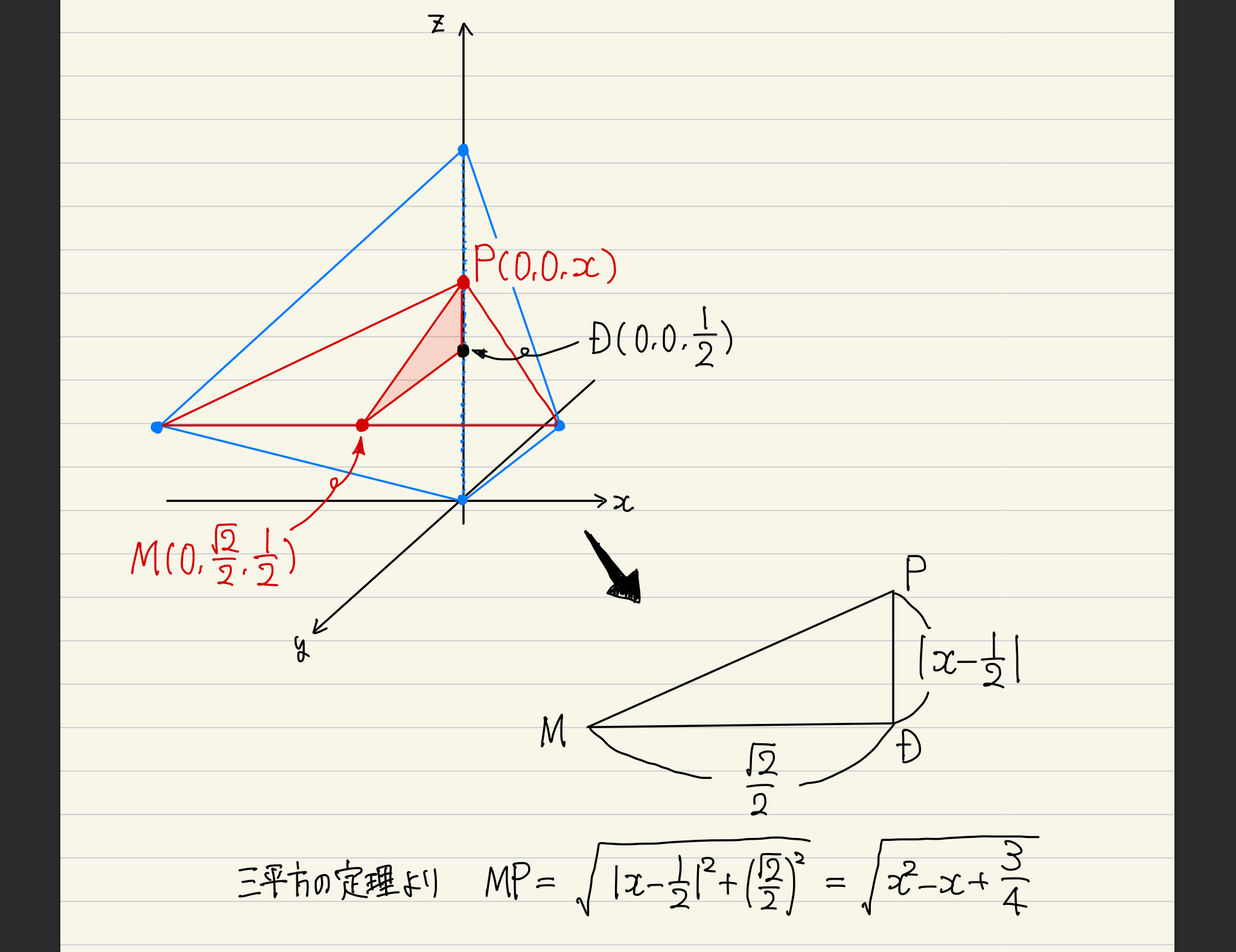



さあ、あとは淡々と作業をするだけで(2)まで解けてしまうはずです。三角形OAPの面積を求めて、最大最小問題を処理しましょう。今回の最大最小は簡単でしたね。実は、最大最小問題にもある程度決まりきったパターンがあるので、またいつか紹介しますね。



解けちゃいましたね。

まあ、少し古い問題ってのもあるのかもしれませんが、とはいえ京都大学。解けて嬉しいですね。おそらく赤本なんかを開いて見てみると、三角比で処理しているんじゃないかなと思いますが(手元にないので確認できない)、それを無理矢理座標で解いてやったぞと。この問題に関して言えば、実は三角比でも簡単に解けるんですけど、まあ座標処理の練習ということでそこは目を瞑ってください。余裕があれば、三角比でも考えてみてくださいね。

細かい記述は端折ってます。間違ってる箇所があれば指摘してもらえると助かります。

では以上。
またやります。