座標で解こう
どうも、フジです。
「座標で解く」暇つぶし数学実践編。
今回は千葉大学の2006年 前期数学 第2問です。これまでは、東大やら京大やらの最難関大学の問題を座標で解いてきましたが、今回は、駿台模試あたりで出題されそうなレベルの入試問題をピックアップしてみました。
千葉大数学を解こう

さて、今回の問題は、三角比を用いて解くことを想定されたような雰囲気。ですが、AB=2でAC=3、そして∠BAC=60°と言われると、△ABCの形は決まっているので、「座標に落とし込みやすいじゃん!」という気持ちになるわけです。ではさっそく、座標で考えてみます(以下の解説を読む前にぜひ自力で挑戦してみてくださいね)。
座標への落とし方を考える際には、原点や直角、対称性を利用することで、なるべく各座標を簡潔にすることを念頭に置きます。
しかし、今回は直角も対称性もないので、次善の策として「変数を突っ込むことになるであろう点が軸上にあれば嬉しいな」と考えました。
この問題であれば、点Eですよね。(2)(3)を見ると線分BEの長さを求めることになりそうなので、余弦定理で辺BC=√7を求めた上で、以下のように、点Bを原点に据えてかつ点Eがx軸上に来るように座標平面上に落とし込めたら、それが理想な気がします。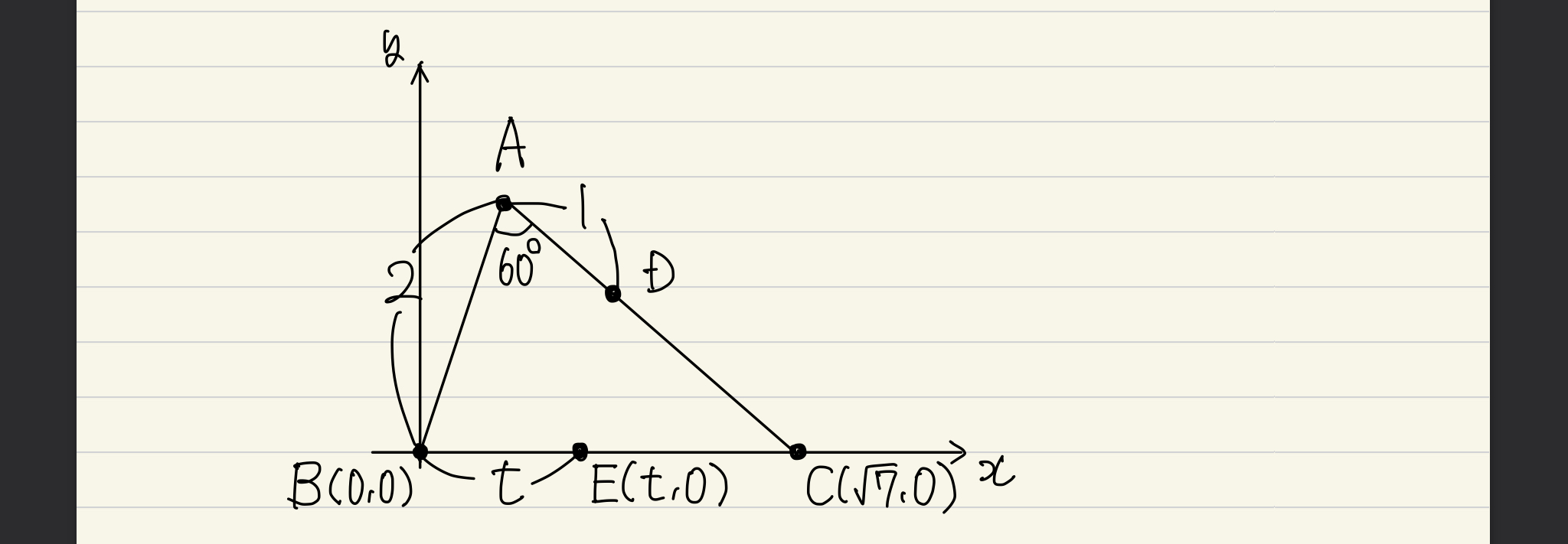
このように配置すれば、点Eの座標が ( t ,0 ) となるので、確かに後の計算が煩雑にならずに済みそう。
しかし、これをやろうと思うと、今度は点A及び点Dの座標を求めるのに若干苦労するんですね。3辺の長さがわかっているのでできないことはないんですが、なんだか面倒臭そうだなあっていう。
というわけで、点Eをx軸上に持ってくることは諦めて、おとなしく∠BAC=60°を利用することにしました。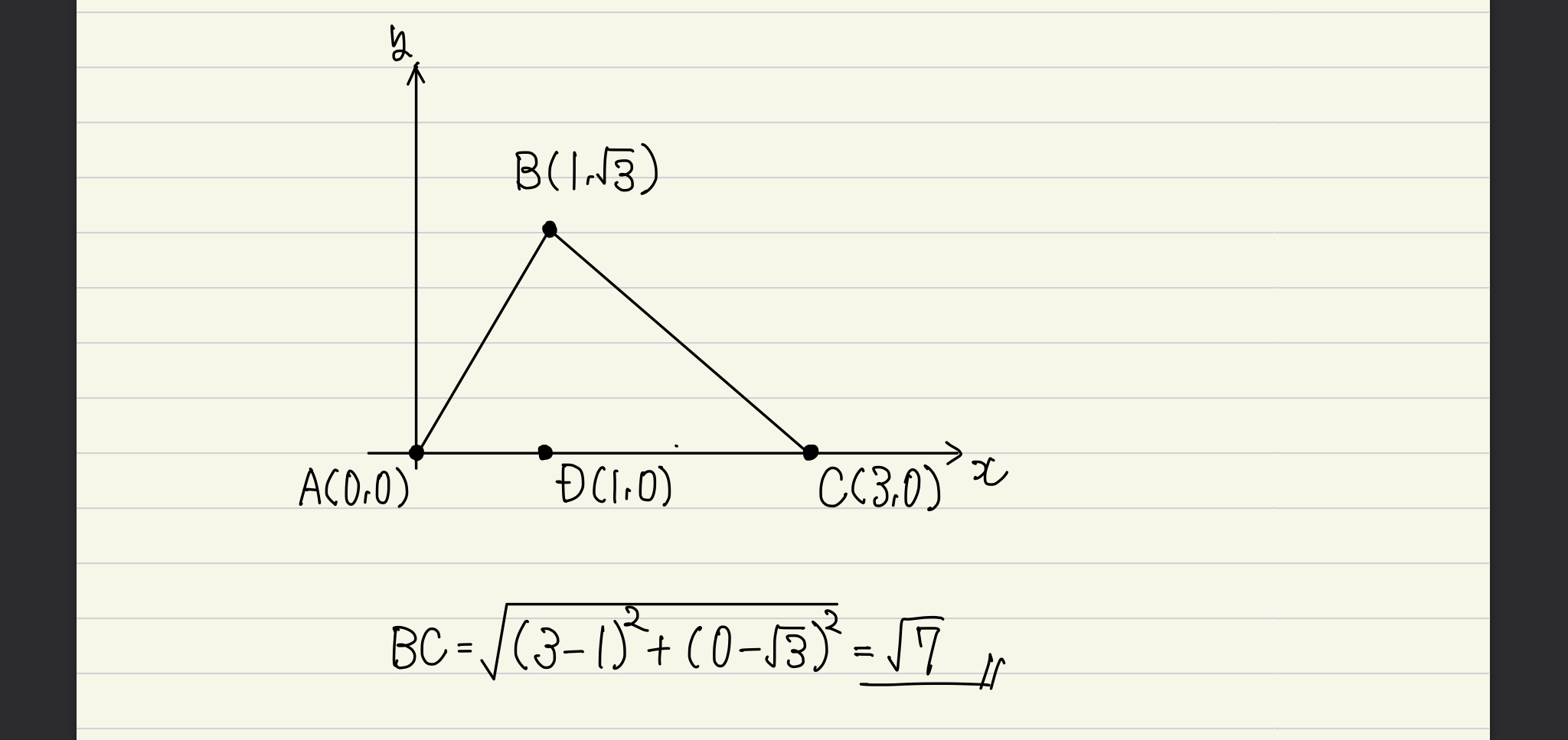
このように配置してやれば、全ての点の座標をすんなりと求めることができますね(点Bの座標は、ABの長さが2ということと、∠BAC=60°から求めましょう)。というわけで(1)はBC=√7です。
続く(2)は、とりあえず点Eの座標さえわかればヨシ。
“線分DEが△ABCの面積を二等分するとき”とありますが、これ、△ABCの面積が算出可能なので、二等分された時のそれぞれ図形の面積もわかっちゃうんですよね。ということで今回は、△CDEに着目。以下のように解き進めます。
点Eの座標を求めた後に、わざわざ線分DEの長さを求めなきゃいけないという一手間。点Bが原点、点Eがx軸上の配置になっていれば…と思わなくもない瞬間ですね。
何はともあれ、答えに辿り着くことはできました。
さて、(3)でようやく点Eが動きます。
“動く点は変数で表す”というのがキホン。ということで今回は、点Eのx座標を t (1≦t≦3)と置いて、△ABEと△DECの面積をtで表そう…という方針です。そうすればあとは、変数1つの最大最小問題を処理するだけ。特に何かを考える必要もなく、無心に手を動かすに尽きます。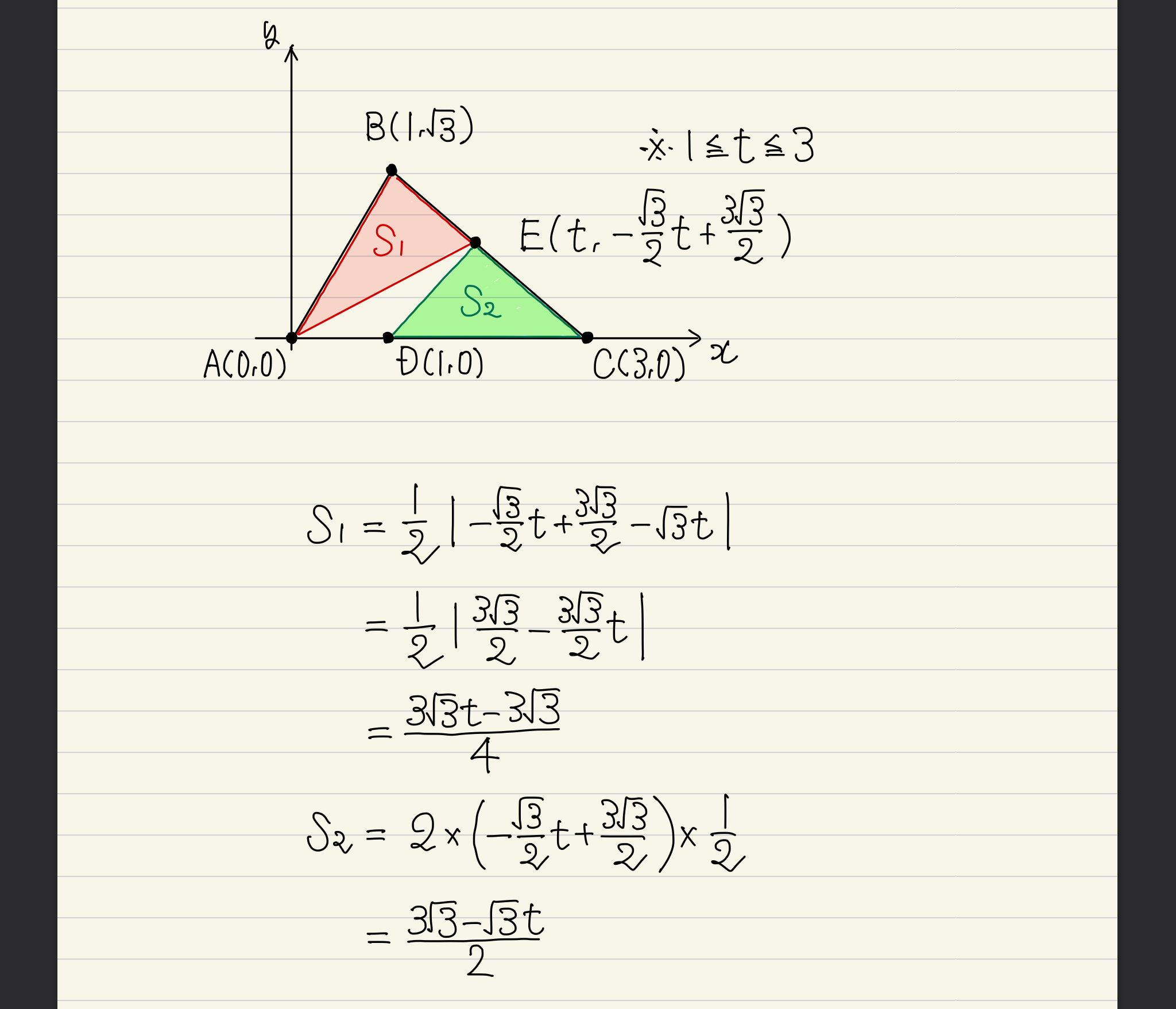
最後はT (△ABEと△DECの面積の積) を求めて、その最大値を弾き出します。書き損ねてますが、tの範囲は 1≦t≦3 です。最大最小問題にあたる時は、常に範囲に気をつけるように。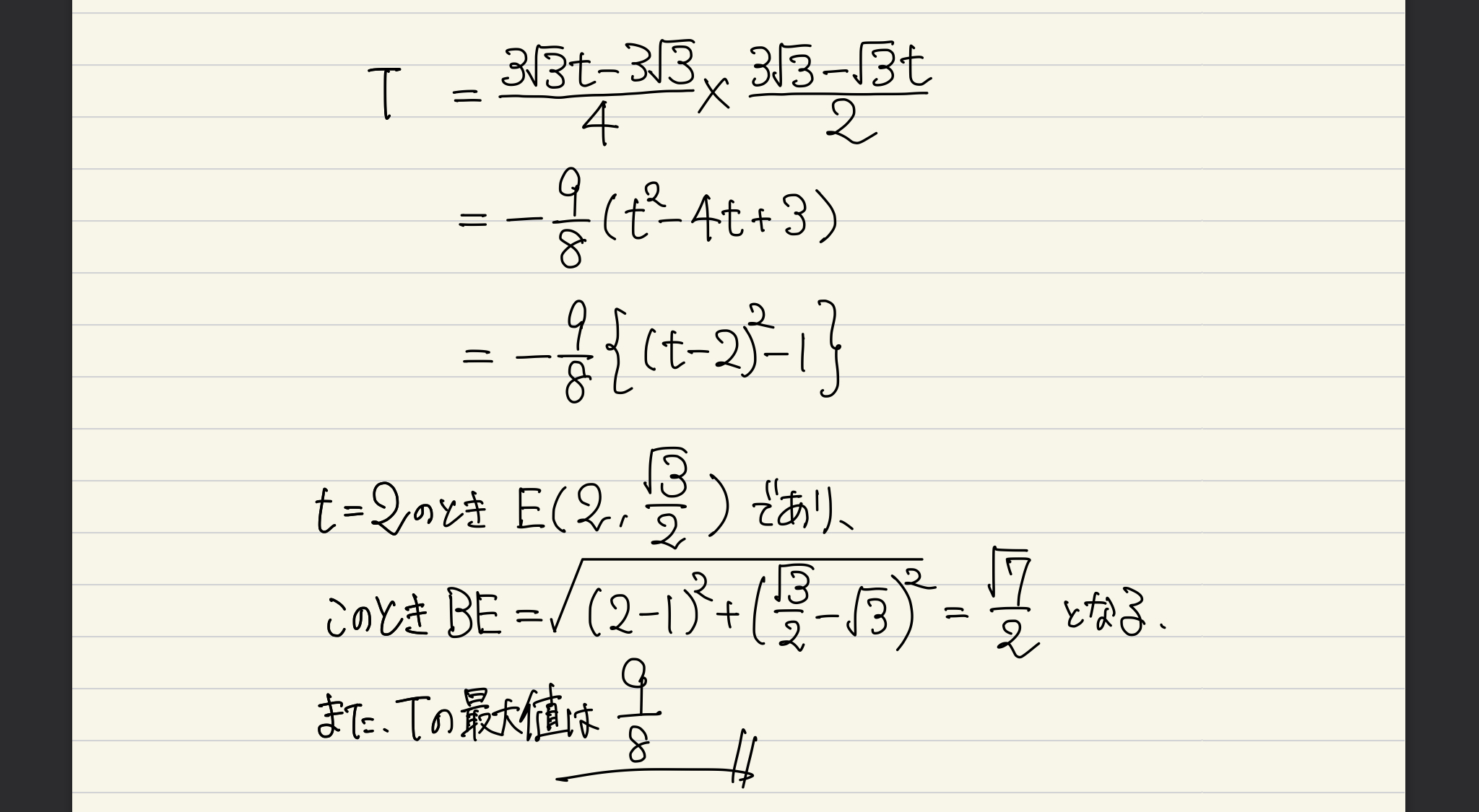
いかがでしたか?
今回はそういう縛りプレイなので、座標を使って解いていますが、おそらく模範解答は三角比で解いてるんじゃないかなと思います。調べたら三角比での解法も出てくるはずなので、余裕があれば是非試してみてください。
最後に余談ですが、問題演習をする際「あ、これもうあとは計算するだけで解けるわ」と感じたら、そこから先を解く必要性はあまりないんじゃないかなと思います。計算しさえすれば求められる答えを求めるのに時間を費やすくらいなら、別の問題の解答方針を考えることに時間を費やした方がいいのでは…と。ただ、もちろんこれは、その後の手を動かす計算部分を正確かつ迅速にこなせるのが前提なので、そこが苦手なのであれば、問題演習の際も常に最後まで解ききるべきかもしれません。
では今回は以上。
【その他の問題】









