座標で解こう
どうも、フジです。
「座標で解く」暇つぶし数学実践編。
今回は一橋大学の問題を座標で解いてみようかなと思います。
一橋数学を解こう

問題はこちらです、2013年の第2問です。問題文中に内積の条件が含まれているので、「ベクトルで解かなきゃ」と思ってしまいそうですが、座標で解きましょう(以下の解説を読む前に、ぜひ自分で考えてみてください)。
まずは内積の条件を噛み砕きます。ありがたいことにOBとOCの長さが与えられているので、∠BOC=60°であることがすぐにわかります。
この時点で「点O、B、Cの3点が固定されていて、点Aが動き回るってことか」と把握できるととても良いです。なお、点Aに関する情報はOA=4のみなので、点Aは点Oを中心に半径4の円を描くことになりますね。それを踏まえて、座標に落とし込んでいきます。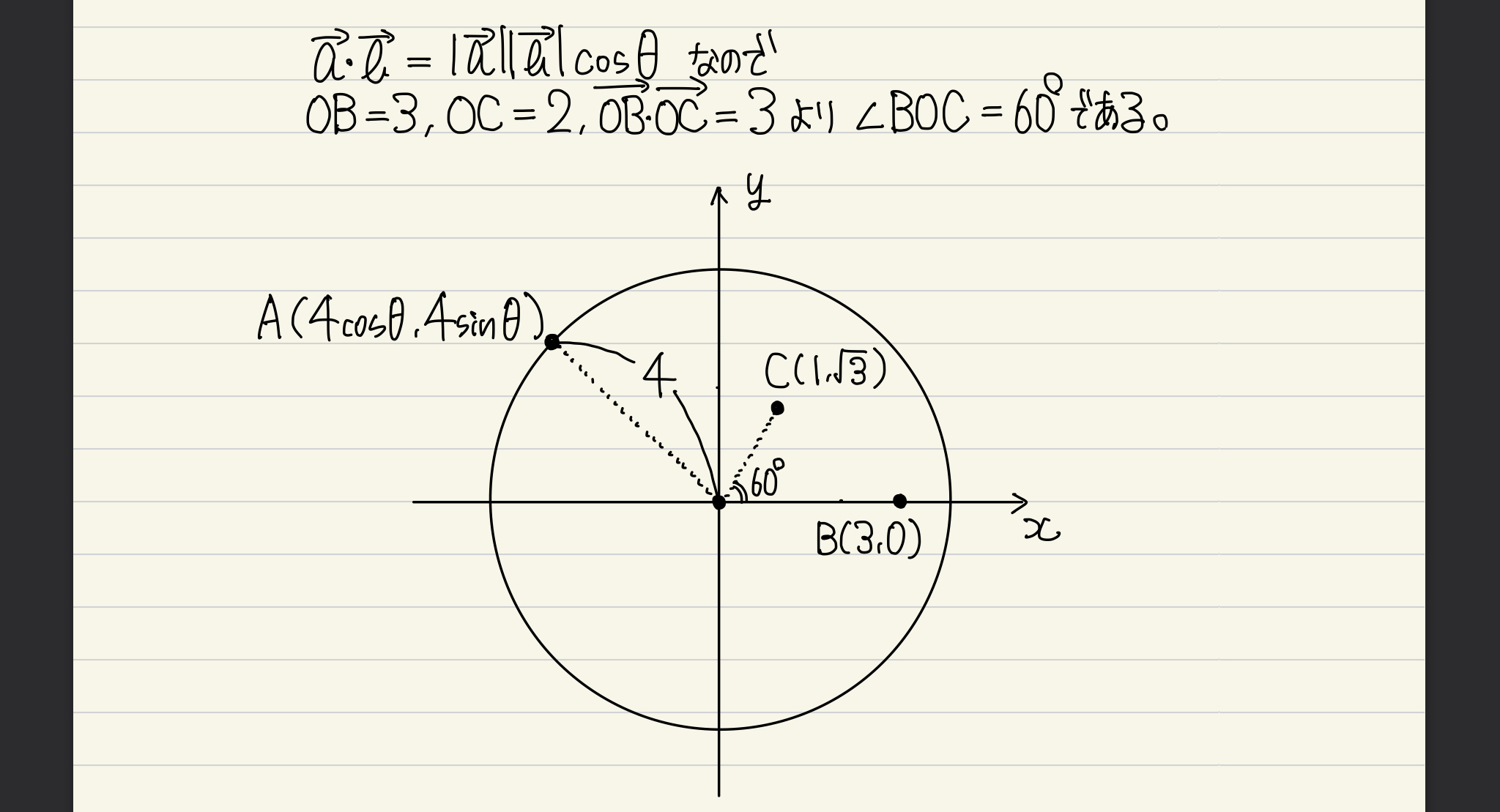
今回は、直角や対称性はないので、「とにかく点Aの座標を簡潔に表したい」という方向性です。
そこで、点Oを原点に持ってきて、点Aの座標を(4cosθ, 4sinθ)とするのが上手いです。 ”動く点の座標を変数で表す”というのが基本テクニックですが、その点が円を描くときは、変数としてθを用いるという手があるということは忘れてはなりません。(p, q) のような置き方をすると変数2つからのスタートとなりますが、θだと最初から1つの変数で表せるので、文字を消去する手間が省けます。
点Aの座標を(4cosθ, 4sinθ)と置けば、解法の見通しが立ちますね。計算を始める前に、解答に辿り着くまでの筋書きをきちんと検討するようにしましょう。
ということで、あとは、三角形ABCの面積をθの関数として表し、その最大最小問題を解くだけです。
前回の記事でお伝えしましたが、三角形の面積の求め方は初等幾何/座標/三角比/ベクトルの4通り。この問題では、初等幾何(底辺×高さ÷2)か座標(1つの頂点を原点に持ってくるやつ)のどちらかが楽だと思います。まぁ一旦初等幾何で。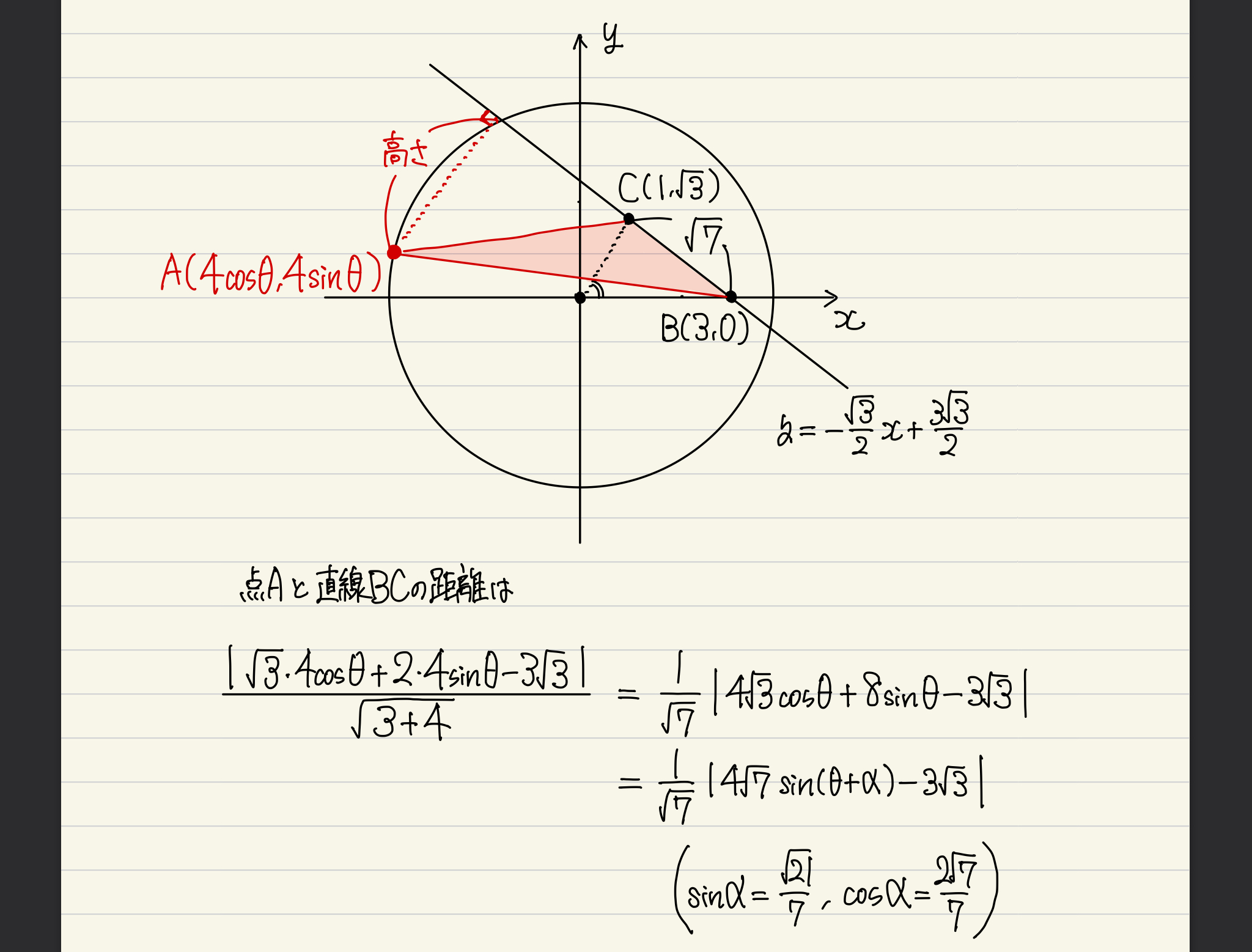
辺BC(長さ√7)を三角形ABCの底辺と捉えると、点Aと直線BCの距離が高さということになります。これは点と直線の距離の公式から求めればオッケーです。そして、高さがわかれば、三角形の面積がわかりますね(sinとcosが混ざっているので、先に合成しておきました)。
あとはθの関数の最大値を求めるだけ。三角関数の合成および最大最小は定番テーマなので、わからなかった方は必ず復習しておいてくださいね。
答えが出ました。
最初の座標設定がうまくいけば、あとは一直線。淡々とやるべきことをこなすだけです。点Aの座標を(4cosθ, 4sinθ)と置いた時点で、ここまでのシナリオをきちんとイメージできていたら素晴らしいですね。
もっと楽に…
三角形ABCについて、点Aの移動で変化するのって結局”高さ”だけなんですよね。つまり、高さの最大値さえわかれば、面積の最大値を計算することは可能なわけです。
高さの最大値については、θで点を表さなくても求められることに気がつきました? 
このように、高さが最大になるのは、点Aが図の位置にくるときですから、「原点と直線BCの距離+4」が高さの最大値であるということがすぐにわかるんです。
というわけで、高さの最大値をパパッと計算して、あとは底辺×高さ÷2で面積の最大値が求められるという流れです。これはきちんと座標に落とし込んだからこそ気がつきやすくなったんだと私は思いますけど、どうでしょう。
座標のこと、好きになりましたか?
では今回は以上。
またやります。
【その他の問題】




