座標で解こう
どうも、フジです。
「座標で解く」暇つぶし数学実践編。
「またかよ!」と思うかもしれませんが、お許しを。ハマっちゃったんです。図形問題めっちゃ面白いです。今回は東京大学の問題を座標で解いてみようかなと思います。
東京大学の2019年 理系数学 第2問です。実はこの問題、少し簡単なバージョンが同年の文系数学でも出題されているんですが、せっかくなので理系の方にしてみました。
東大理系数学を解こう

図形問題を解く時は是非「この問題、座標で処理できやしないか?」と一度考えてみてほしいんですね。
今回のこの問題、問題文中に座標の要素が含まれていないため「三角比の問題かな?」と思うかもしれません。しかしこれ、一辺の長さが1の正方形がベースの問題。これって実は、座標平面上に落とし込みやすいことこの上ないシチュエーションなんです。
ということで一旦、何も考えずに座標平面に置いて、状況を整理してみましょう。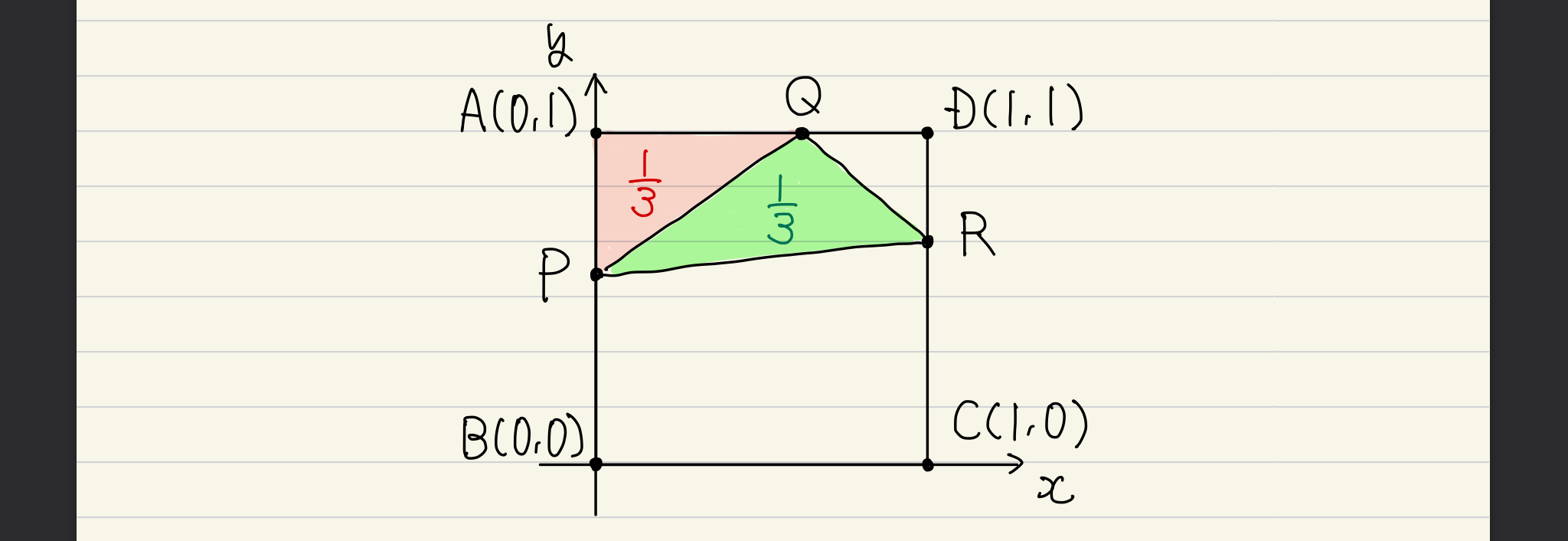
さて、どの頂点を原点に持ってくるのか等は深く考えず、とりあえず配置してみました。
この段階で「点Pの位置が決まれば、△APQの面積が1/3になるように点Qの位置が決まり、点Qの位置が決まれば、△PQRの面積が1/3になるように点Rの位置が決まるのか。つまり、点Pの座標に変数を導入しさえすれば、DR及びAQを含め、全てをその変数を用いて表すことができるので、その先はあとはシンプルな変数1つの最大最小問題になる」ということをぜひ見抜けるようになりましょう(点P、Q、Rは連動しているので、最終的に変数は1つになるという理解)。
数学全体に言えることですが、闇雲に計算を進めていくのではなく、最初におおまかな方針を立てる、ゴールまでの道のりを見据えることが大切です。そして、図形問題を座標平面上に落とし込むと、これが容易になることがあるということです。
ここまで理解できていれば、やりやすそうな以下のような配置に書き換えましょう(これじゃなくても解けるは解ける)。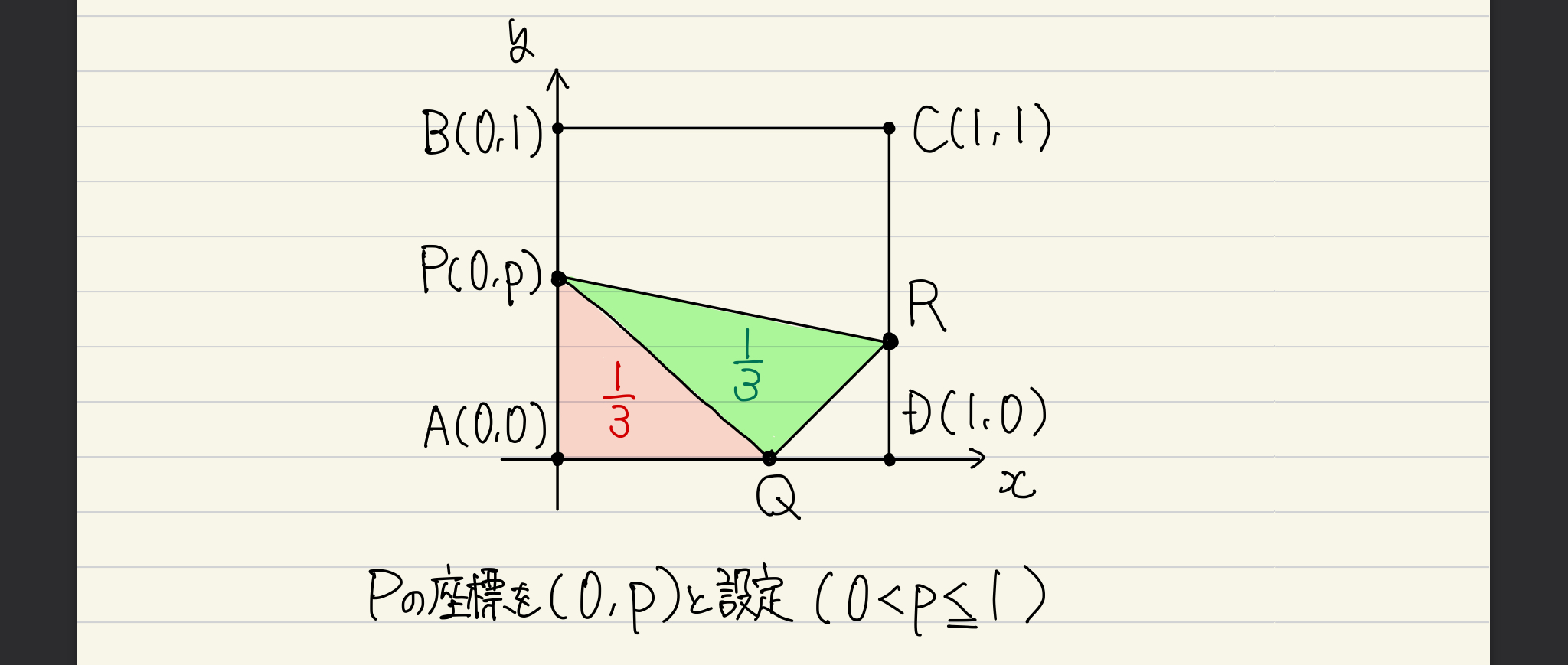
上の方針通り、点Pの座標を(0,p)と置いたので、次は点Qの座標をpを用いて表します。
ここで、pの範囲に変化があることを見落とさないようにしなきゃいけません。文字を消去する際は常に”範囲”のことを考える、これは鉄則です。消える文字に付与された条件を別の文字がちゃんと引き継いであげる必要があるわけです。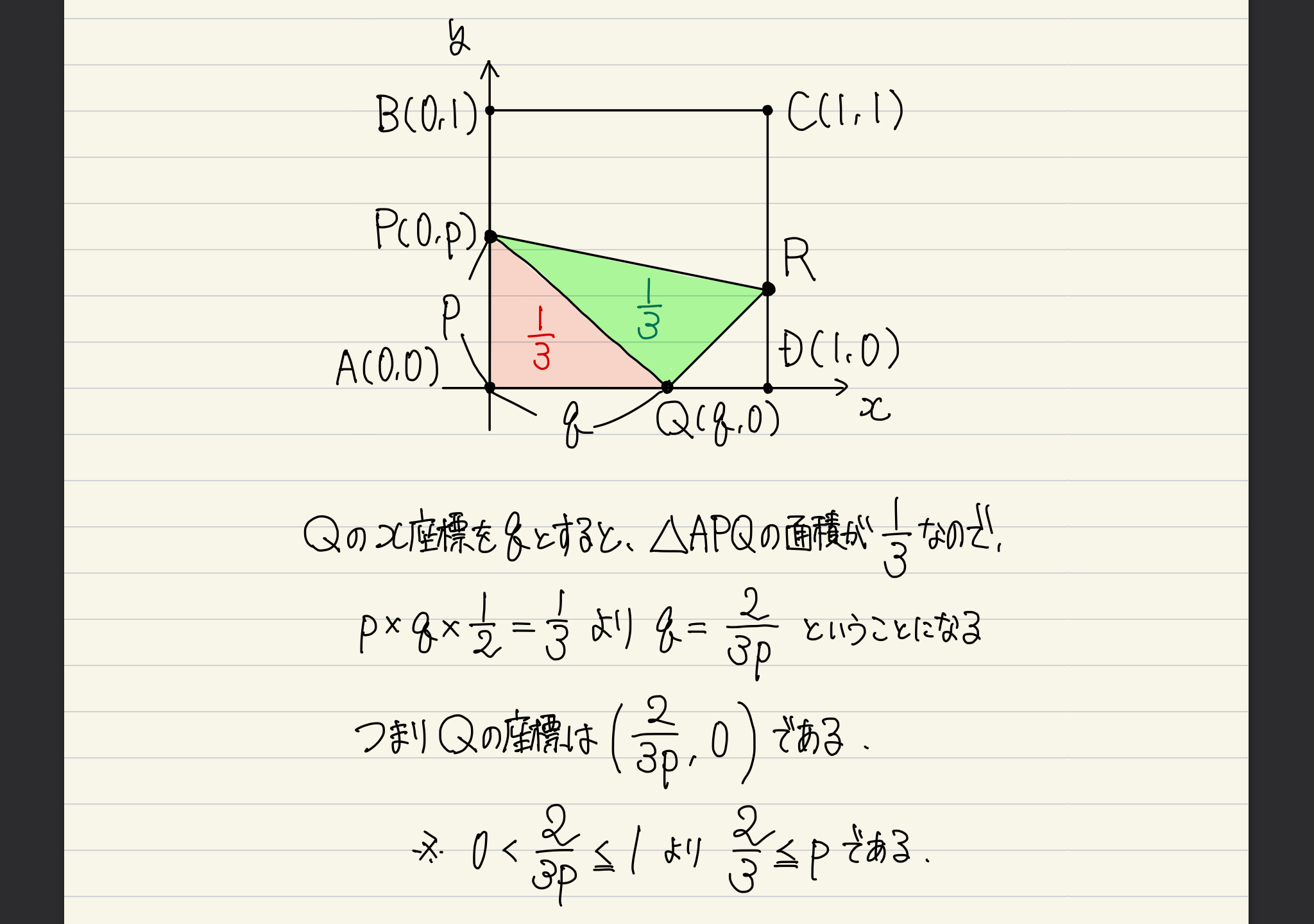
続いて、点Rの座標をpを用いて表しましょう。やり方は様々ありますが、個人的には「台形ADRPから△APQと△QDRを除くと△PQRになるよね」を利用するのが楽かなと感じました。この際もpの範囲にだけはお気をつけを。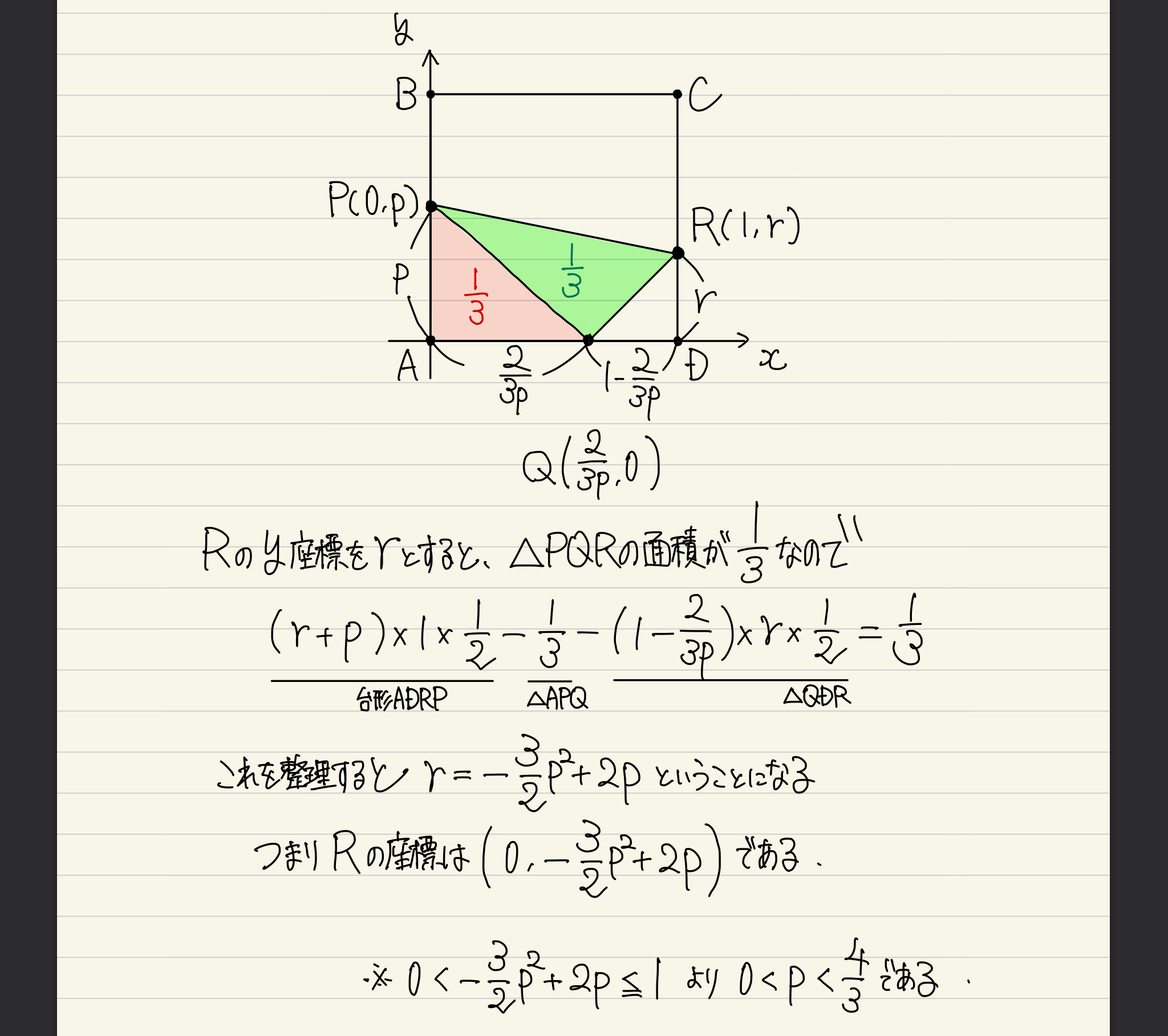
これで、点P、点Q、点Rの座標をpを用いて表すことができました。と同時に、DRの長さ及びAQの長さも、pで表されたことになります。では最後、DR/AQを求め、変数1つの関数の最大最小問題を解きましょう。
答えが出ました。
どうでしょう。最初にうまいこと座標設定ができれば、ゴールまでの道のりをイメージした上で計算を進められるということですね。もちろん三角比でも解くことはできますので、余裕がある方はぜひチャレンジしてみてください。
なお、3次関数の最大最小で躓いてしまった人は、要復習ですよ!
では今回は以上。
【その他の問題】









