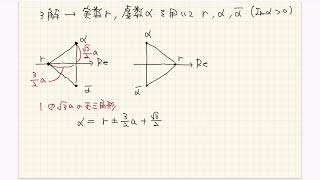
【京大2000】二次方程式の複素数解の大きさ【方程式・複素数】

✅ 東大に合格したい受験生のための個別指導 (人数限定) https://hayashishunsuke.com/lp/lecture-ut/ ✅ 難関大受験生のための公式LINE：https://lin.ee/lI7n1SJ 登録者特典＆受験生向けライブあり 🌟 出版社の方へ https://hayashishunsuke.com/lp/for-publishers/ 数学の書籍を執筆することに強い関心があります。 私に企画のご案内をしてくださる方は，上記ページをご覧ください。 ※これまでの著作：”100年前の東大入試数学” (KADOKAWA) ℹ️ 林俊介のプロフィール https://hayashishunsuke.com/profile/ ・栄東中→筑駒高→東大理一→東大物理学科卒 ・東大二次の数学で 9 割獲得し現役合格 ・2014年 日本物理オリンピック金賞 ・2014年 東大実戦模試物理1位 ℹ️ ご注意いただきたいこと ・解説は林俊介独自のもので，大学公式のものではありません。 ・書籍等の紹介には Amazon アソシエイトリンクを用います。 2000年度の京大理系数学より，2 次方程式の複素数解に関する問題をピックアップ。 (1) では，放物線（の半分）と直線が共有点をもつような定数 a の範囲を求めます。 直線が a の値によらず通る定点の存在に気づくことができれば，苦労せずに解ける問題でしょう。 この問題に限らず，パラメータの値によらず曲線や直線が通る定点というのは，問題を解くうえで役に立つことが多いですし，少なくともグラフを図示するうえでは確実に役に立ちます。 (2) では，2 次方程式の複素数解の絶対値がテーマになっています。 一見 (1) とは関係ないように見えますが，両辺を a^2 で割り算することで，(1) が使える形になりますね。 直線と放物線（の半分）の共有点が実数解と対応しているわけですから，共有点の x 座標が大きい方が β ということになりますね。 ただし，(1) が使えるのはあくまで実数解が存在する場合のみ。虚数解の場合は別途議論が必要なので注意しましょう。 実数解をもつときの |β| の最小値を (1) を利用して求め，虚数解をもつ場合の |β| はそれよりも大きくなることを証明すれば OK です。 (2) では虚数解をもつ場合もあるので，そこで混乱して手が止まってしまう人も多いのではないでしょうか。 ただ，特別なテクニックが必要というわけではないので，差がつく難問という印象です。 ---------- ＜目次＞ 00:00 2000年 京大 理系数学 [2] 00:45 (1) C: y = √x のグラフ 02:12 (1) 直線 l が通る定点はあるか？ 03:48 (1) 直線 l の傾きの範囲は？ 06:04 (1) 答えのイメージ 07:44 (1) x ≥ 1/2 では交点をもたない 10:11 (1) 原点を通るとき＆接するとき 14:54 (1) 条件をみたす a の範囲 16:47 (1) 解法のまとめ 19:05 (2) (1) との関係は？ 20:19 (2) 方程式 (★) が実数解をもつとき 26:45 (2) 実数解をもつ場合のまとめ 28:23 (2) 方程式 (★) が虚数解をもつとき 32:05 (2) 結論と解法のまとめ 35:01 (2) おわりに