共役

概要

を実数とするとき、複素数 に対して、 を、複素数 の共役な複素数という（共役な複素数はバーを付けて、 で表す）。

最初の難関はこの漢字の読み方。「きょうえき」と読みたい気持ちをグッとこらえて、 「きょうやく」 と読む。クラスで「きょうえき」と読む友達がいたら、優しく教えてあげよう。

例えば、 と共役な複素数は となる。

性質

また、共役な複素数の性質として、 元の複素数との掛け算は必ず実数になる。例えば、

さらに、共役な複素数の計算については、以下の性質が成り立つ。

• 足し算

• 引き算

• 掛け算

• 割り算

最後は分母の共役な複素数を分母分子にかけて、 分母の実数化を行った。

上の例で分かる通り、共役を取って四則演算を行っても、四則演算のあとで共役を取っても、 値は同じになる。

あと、 係数が実数である 次方程式が虚数の解を持つとき、その共役な複素数も必ず解になる。証明は、例えばこちらの古賀さんの「複素数の基本性質」の動画を確認しよう。

発展（数学III：複素数平面）

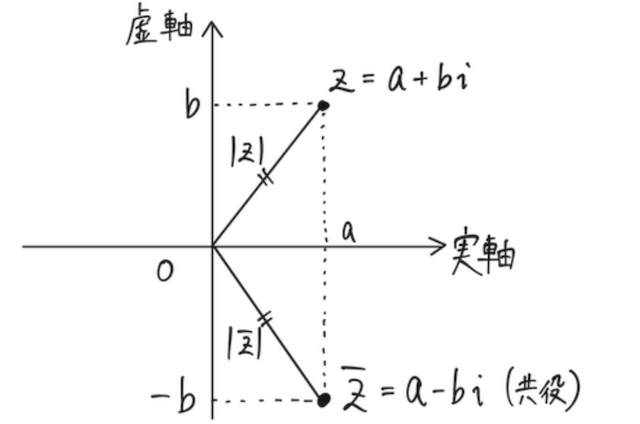
複素数平面上では、共役な複素数は、元の複素数と実軸に関して対称な位置にあり、 原点からの距離は等しい