動く導体棒

動きまくる導体棒

電磁誘導の分野で、電流を流す導体棒が動く問題はめちゃくちゃよく出てくるので、重要テーマを押さえておこう。特にこの2つ。

• 誘導起電力の求め方（2種類）
• エネルギーの関係（やや発展）

長い内容になるが、流れを理解しておくべきテーマなので、じっくり考えながら見ていこう。ここが自分のものにできると、電磁誘導が得意分野になる。

※ レンツの法則とファラデーの電磁誘導の法則についての知識が前提となるので、忘れた人は先に復習しておこう。

誘導起電力の求め方

まずはシンプルにこの設定で考えてみよう。

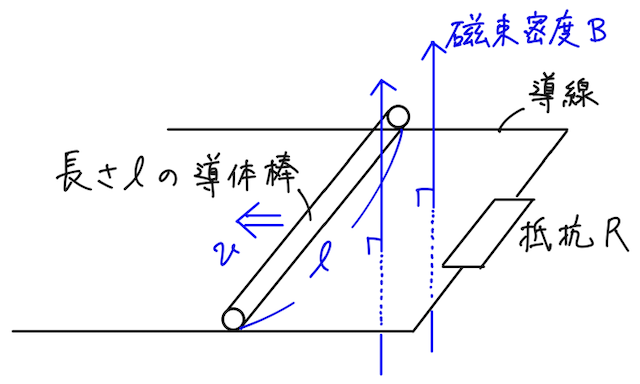
抵抗値 の抵抗と、速さ で左に動く導体棒が導線でつながっていて、磁束密度 の磁場が回路の下から上に貫いているとする。

このとき、この導体棒に生じる誘導起電力の向きと大きさを求めよう。ここでは重要な2通りの考え方を紹介する。

レンツ＋ファラデーで考える

まずは、誘導起電力の向きを考えるレンツの法則と、誘導起電力の大きさを考えるファラデーの電磁誘導の法則を用いて求めてみよう。

今回の状況で、導体棒が動くと、回路を貫く上向きの磁場が増える。よって、「誘導起電力は、それによって流れる誘導電流のつくる磁場が、変化を打ち消すような向きに生じる」というレンツの法則より、下の図のような向きに誘導電流が流れることになる。

（どっちに流れると下向きの磁場が増えるか、を考えよう！）

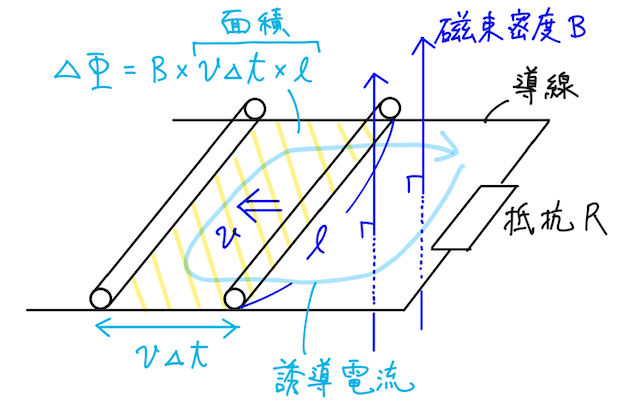
さらに、 間の磁束の変化 を考えると、回路の増える面積は であるので、それに磁束密度をかけて

と求められる。（磁束の向きが回路の増える面に対して直交していることに注意しよう！直交していない場合は最後に補足）

よって、ファラデーの電磁誘導の法則より、誘導起電力の大きさ は

と求められる。

この誘導起電力により、回路には誘導電流が流れ、その大きさはオームの法則から

となる。

ローレンツ力で考える

では、この誘導起電力や誘導電流を、導体棒内の電子の動きから考えてみよう。実は、それでも同じ結果を得ることができる。

導体棒内の電子の左向きの速度は、棒と同じく であり、磁場が下から上にかかっているので、電子の電気量 にはたらく、導体棒の向きのローレンツ力の大きさ は、

と求められる（下で補足あり）。

さらに、電気量がマイナスであることに注意して、ローレンツ力の向きは下図の通り となる。

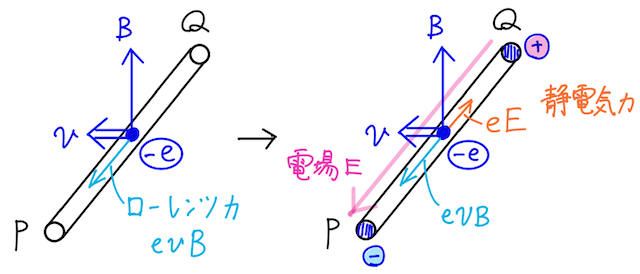
よって、電子は運動を始め、 側に負の電荷がたまるようになるので、 の向きに電場が生じる。その大きさを とおく。

導体棒内の電子は、もちろんこの電場から静電気力を受ける。電気量がマイナスなので、静電気力の向きは の向きで、大きさは となる。

電子が 側にたまるにつれて は大きくなっていき、どこまでいくかというと、静電気力が上で求めたローレンツ力とつり合うまで続くことになる。

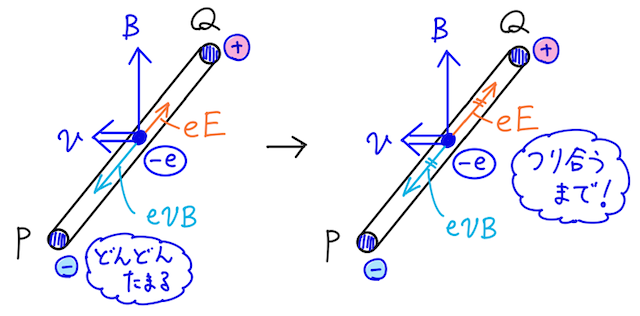
このとき、力のつり合いから電場の大きさは

と求められる。

よってこのとき、導体棒の両端の電位差は、 の方を高電位側として

となる。（わからない人は一様電場の電位差の式を復習しておこう！）

なので、この両端をつなぐ抵抗がつないであると、抵抗を通って電流が流れるので、電流の向きは下記の通り。

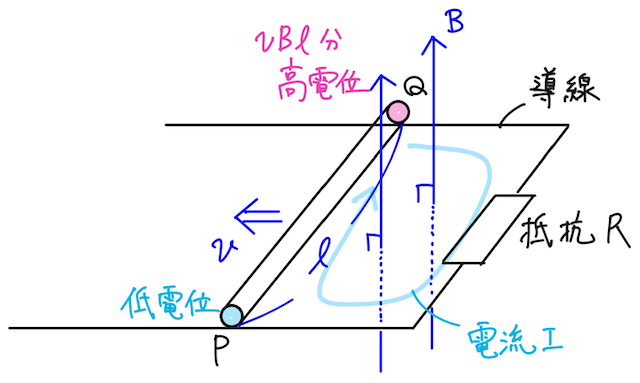
よって確かに、レンツの法則とファラデーの電磁誘導の法則を使って考えたときと、同じ結論となる！

エネルギーの関係（やや発展）

では、誘導起電力の向きや大きさ（誘導電流の大きさ）の求め方がわかったところで、時間とともにエネルギーがどのように移り変わるかを考えてみよう。入試でもこれでもかというくらい出題されるテーマ。

回路に起電力 の電池がつながっており、導体棒に重りをぶら下げて、導体棒が左に速さ で動いている下の状況を考える。

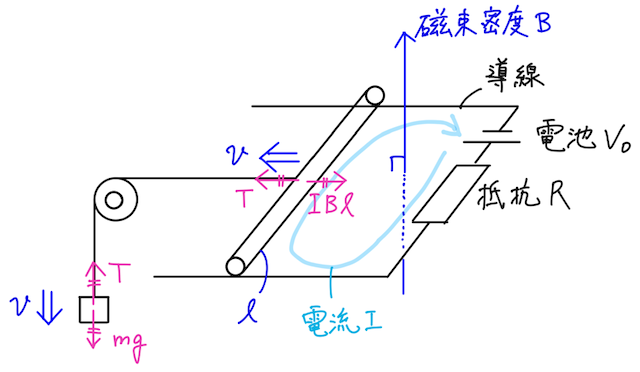
まずは、この状況で、何が起こっているか（なぜ等速で動けるのか） を捉えるのが超重要。

今回は電池と抵抗が導線と導体棒でつながっていて、そもそも導体棒が動いてなくても電流は流れるが、導体棒が動いていることによる誘導電流も生じており、それらを合わせた電流を とする。

このとき、導体棒のところで、電流 が磁場から受ける力が右向きにかかっている。（もちろん他の導線のところでも力がかかっているが、動かないとして考えない）

この力と、重りの重力がつり合っている（正確にはそれぞれが張力とつり合っている）ため、導体棒と重りは等速で運動できているのである。

ちなみに補足で、このような回路で電池がつながってないケースもよく出題される。このときは、重りをぶら下げた瞬間には電流が流れておらず、導体棒は左に加速していく。で、左に動いていくと誘導電流が流れはじめ、それにより、導体棒のところで誘導電流が磁場から受ける力が右向きにはたらきはじめて、この場合でも結局重力とつり合って落ち着く（等速運動になる）ことになる。

では、状況をつかんだ上で、この回路でキルヒホッフの第二法則を立式すると、上で見た、導体棒での誘導起電力の向きを踏まえて、

となる。時間 での変化を考えると、全ての辺に と を掛けて整理して、

を得る。

それぞれの項の意味を考えると、

• → は電池が流した電気量であり、それに電池 の起電力がかけられているので、これは電池 のする仕事を表す
• → は導体棒の動いた距離であり、電流が磁場から受ける力（）と動く方向は逆なので、これは電流が磁場から受ける力が、導体棒にする負の仕事を表す
• → これは抵抗で発生するジュール熱を表す

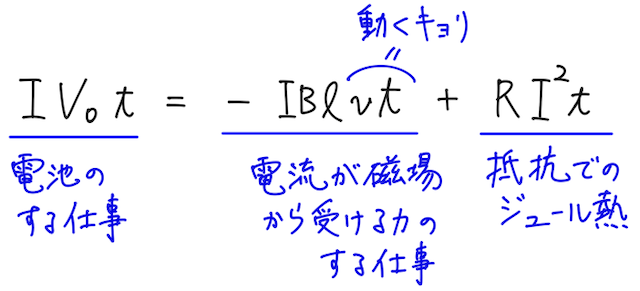
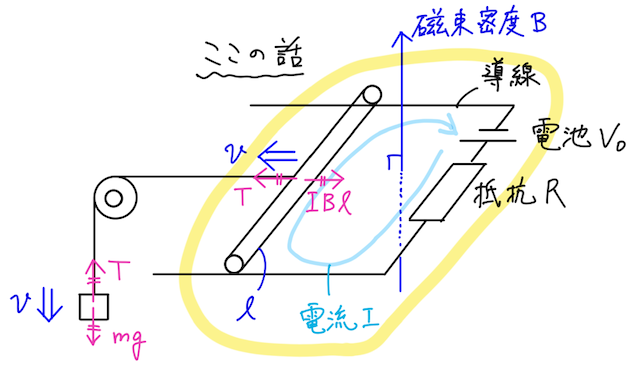
一方で、重りの重力と、導体棒で電流 が磁場から受ける力とのつり合いより（正確には、それぞれ張力との力のつり合いにより等しくなっているだけ）

であるので、全ての辺に と を掛けて整理して、

を得る。

こっちも、それぞれの項の意味を考えると、

• → 上と同じく、これは電流が磁場から受ける力（）が、導体棒にする負の仕事を表す
• → は重りが下がった距離なので、これは重りの重力による位置エネルギーの変化を表す

つまり、電流が磁場から受ける力のする負の仕事によって、重りの重力による位置エネルギーが減っていることを意味する（注1）。

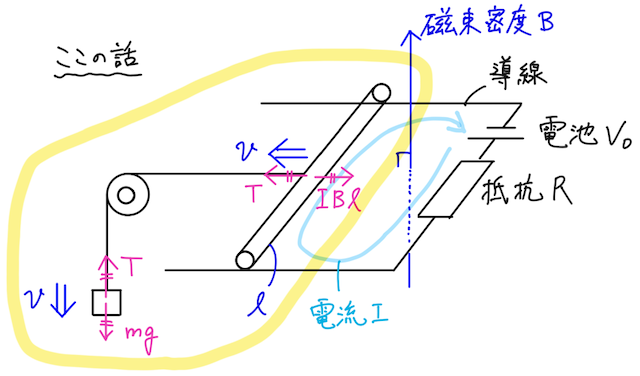
ここで、 式と 式を足して整理すると、

となって、電流が磁場から受ける力のする仕事は相殺される。

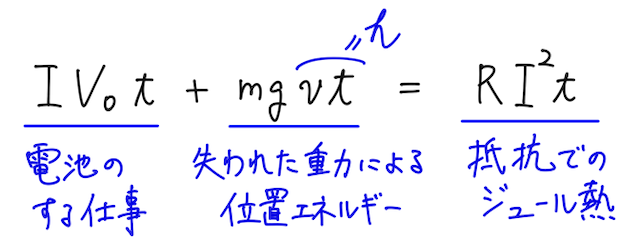
足した式を見ると、この運動を全体として見たときに、電池のする仕事と、失われた重力による位置エネルギーが、抵抗でのジュール熱として消えていくことを意味する（注2）。

（注1）もちろんそれぞれの張力 も仕事をしている。じゃあなんでこの仕事はエネルギーの収支に出てこないの？と思うかもしれないが、張力が導体棒にする仕事と、張力が重りにする仕事は、ちょうど向きが逆になり相殺するので、エネルギー収支には出てこない。

（注2）ちなみに、ここでは重りをぶら下げて等速にしたが、

• 重りをぶら下げずに導体棒が減速するモデルを考えると、第2項は、失われた重りの重力による位置エネルギーではなく失われた導体棒の運動エネルギーとなる
• 重りではなく、手で頑張って引っ張りながら導体棒を等速で動かすモデルを考えると、第2項は、重りの重力による位置エネルギーではなく手が導体棒にする仕事となる

ので、興味のある人は考えてみよう。

では、最後に補足を2つ。

補足①：磁場が斜めに貫く場合

磁場が斜めに貫く場合には、磁場に対して垂直な成分で面積を考えて磁束密度に掛け算する。つまり、下のように磁場の向きから だけ傾いた面を導体棒が動くとすると、

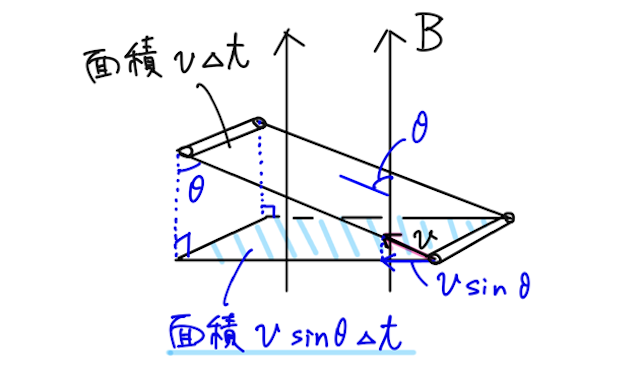
磁場に垂直な成分を考えて、磁場が貫く面積は となるので、誘導起電力の大きさは、

と求められる。

補足②：ローレンツ力のもう片方の成分

鋭い人は、「あれ、でも導体棒内の電子って斜めに動いてね？」と思うかもしれない。

その通りで、導体棒は左に動くが、電子は導体棒内も動いているので、上から見るとこんな感じで電子は斜めに動いており、それに垂直にローレンツ力がはたらく。

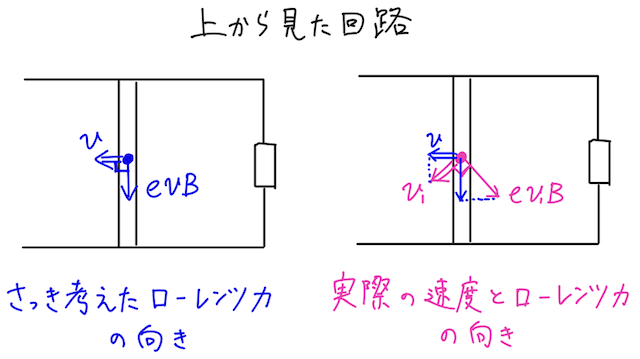
つまり、さっき考えた、左向きの速さに対する導体棒の向きのローレンツ力は、単なる一つの成分にすぎない、ということを理解しよう。

そうすると、ローレンツ力のもう一つの成分はどういう意味を持つのだろうか？

実はこの総和が、電流が磁場から受ける力 を表すことになる。

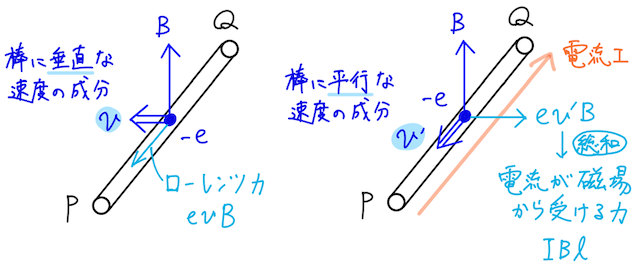
実際に計算して確かめよう。

電子の導体棒の向きの速度を とし、導体棒の断面積を 、導体棒内の単位体積あたりの自由電子の数を とする。

このとき、1個の電子にはたらく右向きのローレンツ力の大きさは

となるので、導体棒内の電子にはたらく右向きのローレンツ力の総和 は、

となる。ここで、電流 は

と表せるので（この理由がわからない人は電流の用語の方で確認しよう）、確かに

となり、電流が磁場から受ける力を表していることがわかる。

＜余談＞

ここまで読みきった方は本当にお疲れさまでした。。。この用語を書いたあと、ふと電車の吊り革をつかんだ状況って電流と磁場の絵に似てるなと思い、テンションが上がっておりました。休息が必要だなと思いました。