キルヒホッフの法則

概要

物体の運動を調べることができる運動方程式、気体の状態を調べることができる状態方程式、これらに並んで、回路の各部位の様子を調べることができる法則が、次のキルヒホッフの法則である。

回路の問題は、このキルヒホッフの法則の式を立てて解けば、基本的に全ての問題は解けるという、優れもの。

第1法則「回路の任意の分岐点について、流入する電流の総和は、流出する電流の総和に等しい」

第2法則「回路の任意の閉じたループについて、 周するとき、起電力の総和は、電圧降下の総和に等しい」

まずそれぞれの注意点を補足して、そのあと例題で使い方を確認しよう。この法則は使えてナンボ。

第1法則について

回路のある分岐点から、流出する方向を正、流入する方向を負にとると、第1法則は 「分岐点について、電流の代数和をとると になる」 と表現することもできる。

代数和とは、符号まで含めて和をとることで、簡単に言えば正負の数を含んだ足し算のこと。

ある分岐点に導線が 本繋がっていて、 本から 流入し、 本から 流出していたとする。残りの 本から流出する電流を、 とすると、第1法則から

となるので、残りの 本からは 流出していることがわかる。

この例でもわかる通り、符号がめちゃくちゃ大事。自分で決めた符号（流出が正、など）のルールを貫いて、式を立てよう。変数をおくときは、自分が正の向きと決めた方向を正の値に対応させる。

第1法則は、「(分岐点での)電荷保存則」 とも考えられる。電流はすなわち電荷の動きであるから、回路の分岐点で電荷が無くなったり、突然増えたりすることはないよ、ということ。

ちなみに「電荷保存則」という考え方はコンデンサーを含む回路でとても役に立つ考え方で、この場合の電荷保存則は、回路で孤立している部分の電荷の和が保存する、ということを意味する。

第2法則について

これは別名 「回路方程式」 と呼ばれ、回路の問題で大活躍する法則。

起電力や電圧降下は、自分で定める向きによって負にもなり得るので、上で考えた「代数和」という言葉を用いて、「回路の任意の閉じたループについて、 周するとき、起電力の代数和は、電圧降下の代数和に等しい」と書かれていることもある。

こちらも符号がとても大事で、電流の向きや、ループの1周する向きはどっち周りで置いても良いが、自分で決めた向きに沿って忠実に式を立てよう。

起電力については、電源の負極側から正極側に進む向きを正、正極側から負極側に進むときは負となり、電圧降下については、ループを 周する向きと電流の向きが同じときは正、逆向きのときは負ととる。（慣れるまでは、電流の向きとループを 周する向きはそろえた方がわかりやすい）

このような簡単な回路では電流の向きはすぐに時計回りとわかるが、もっと複雑な回路で、電流の向きがわからない場合は、自分で勝手に向きを決めて、負の値が出てきたら「ああ逆向きだったのね」と理解すればOK。

例題

【問】以下の回路で、各抵抗を流れる電流の大きさを求めよ。ただし、 は抵抗、〜 は各電池の起電力とする。

【答】こんなパッと見、わけがわからない回路でも、文字を置いて、キルヒホッフの法則に沿って立式していけば必ず解ける。

まずは、各抵抗を流れる電流の向きと値を定める。どっち向きが正でもいいが、ここではとりあえず電池の向きにそろえて置いている。

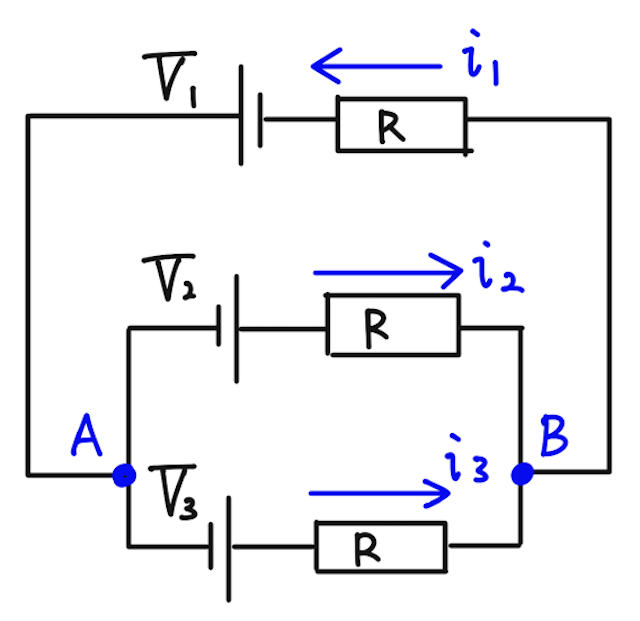
キルヒホッフの第1法則より、分岐点 について、

流出する方向を正として立式してみたけど、どっちでも構わない。

分岐点 もあるが、 と同じ式になるので、どっちかだけ立式すれば良い。

そして、下の つのループを考えると、キルヒホッフの第2法則より、

上の式がループ 、下の式がループ に対応する。抵抗での電圧降下については、オームの法則 を用いている。

符号にとにかく注意！ループの向きは自分で決めて、起電力や電圧降下の符号については、わからなくなったら上の定義を復習しなおそう。

そして、未知数は 〜 の つ、式が つなので、これで解ける。

実際連立方程式を解くと、

求められているのは、電流の大きさなので、絶対値をつけておけば、この問題の答えとなる。（ や については、正負どちらもありうる）

あれ、ループもう一個あるよね？と思った方もいるかもしれないが、ここでは2つのループで第二法則が成り立てば、もう1個のループでも自動的に成り立つので、2つ考えとけばOK。気になる方はもう1個のループも確かめてみよう。