電流

概要

電荷の流れを電流という。まずは向きと大きさを定義しよう。

正電荷は高電位の側から低電位の側へと移動し、負の電荷は逆向きに移動する。そこで、正電荷が流れる向きを電流の向きと定義する。

さらに、導体の断面を単位時間（ 秒）に通過する電気量を、電流の強さと定義する。

つまり、時間 の間に通過する電気量を とすると、電流の強さ は、

となる。さらっと書いたが、電流の単位はアンペア であり、これについては、補足で後述する。

これで、向きと大きさの定義が完了した。

この電荷との関係はとても大事で、時間をどんどん短くしていくと、

となり、電流は電荷の時間微分となることが分かる。これはややこしい回路の問題を解く上で、とても大事な式となる。

（細かい補足）

ここでは、電流の強さを としたので絶対値がついているが、電磁気の問題では、どっちに電流が流れるかわからないので、自分で電流の正の向きを定めた上で、電流を とおくことも多い。

このとき、例えばコンデンサーの充電中に、極板に溜まっている電荷を とおくと、 が増える向きと、電流の正の向きは揃えるようにしよう。

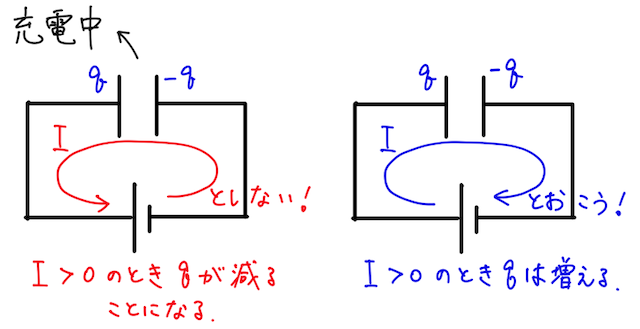
そうすると、正の向きが揃うので、絶対値を外して

と書けることになる。

発展

ややこしいのが、電流というのは通常、原子核に束縛されない自由電子（化学の金属結合で出てくるやつ！）の流れのことであり、自由電子は負の電荷を持つので、実際に導体内で起こっている自由電子の流れと、ここで定義される「電流の向き」は逆になる。

ここが本当にややこしいので、下の例を通して理解してほしい。

【問】断面積 の導線の中を平均の速さ で運動する自由電子によって流れる電流の向きと強さ を求めよ。ただし、単位体積あたりの自由電子の数を 、電子の電荷を とおく（つまり電気量は ）。

【答】まず、電流の向きを考える。定義から、正電荷が流れる向きが電流の向きなので、負の電荷である自由電子の動く方向とは逆向きが電流の向きとなる。

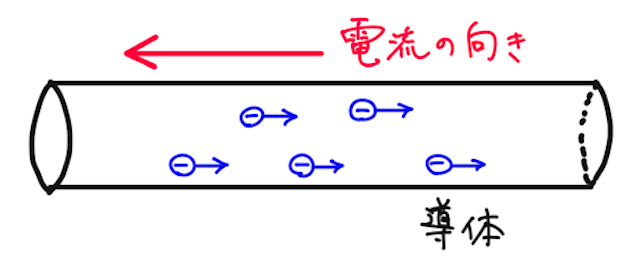
では、電流の強さ を求めよう。まずは時間 を自分で勝手に設定する。この時間で、導線の断面を通る自由電子の数を求めると、断面から長さ までのところにある自由電子が通ることになるので、個数は、

となる。

つの自由電子の電気量は なので、断面を通る電気量の大きさは、電気量に個数をかけて、

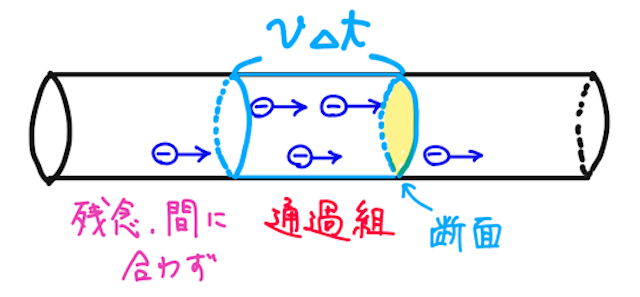
となる。よって、電流の強さの定義から、 は

と求められる。

「え、でも電子って加速されるから、 って時間変化するんじゃないの？」と思った鋭い方は、さらに詳しく背景を学べる東大物理学科卒のひぐまさんの動画を確認しよう。

補足

これまでの単元では、電荷の移動がなく固定された電荷分布を考えていて、つまり静電気学がメインであった。ここからの単元では、電荷が動く、つまり電流についても考察できるようになっていく。

歴史的には、 年にボルタが電池を発見して初めて人類が定常電流というもの手にした。なので歴史で見ると、電流を扱っているのは実はわずか 年に過ぎない。

また、電流の単位について、実は 年にアンペア の定義が改定された。（興味ない方は飛ばしちゃってください）

それまでは、「 本の無限に長い電線が間隔 で平行に置かれていて、どちらにも同じ大きさの電流が流れているとき、電線間にはたらく力が あたり のときの電流を とする」と定義されていたが、新しい定義では、まず、電気素量 （電気量の最小単位のことで、 つの陽子がもつ電荷の大きさ）の値を

と定義する。この定数を用いると、 クーロン は

となり、 アンペア は 秒 間に電子が

通過したときの電流と定義されることとなった。これから分かる通り、

という単位間の関係式が成り立つ。これは電流の強さの定義（単位時間あたりの通過する電気量）からも納得できる。