電力量

概要

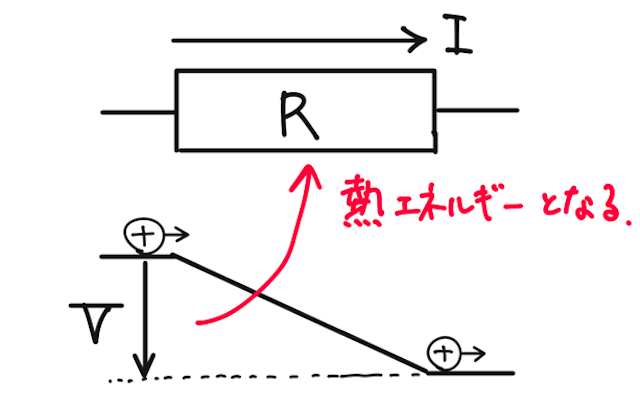
抵抗に電流が流れると、熱が発生する。これはなんとなくイメージでもわかるかと思う。これを式で求めてみよう。

抵抗の両端の電圧（電位差） を とする。抵抗に、電流 が時間 流れたとすると、電流の定義から、高電位側から低電位側に

だけの電荷が移動することになる。よって、この間に電荷が失う静電気力による位置エネルギーは、電位の定義から、

と求められる。この、失った位置エネルギーを消費電力量、もしくは単に電力量という。上の流れから分かる通り、単位はエネルギーと等しくジュール である。

この失った位置エネルギーの分だけ電流が仕事をすると考えられ、これは全て抵抗で発生する熱に変わる。これをジュールの法則といい、発生する熱をジュール熱という。つまり、ジュール熱も で求められる。

抵抗を とすると、オームの法則より

なので、電力量及びジュール熱は、

でも求められる。

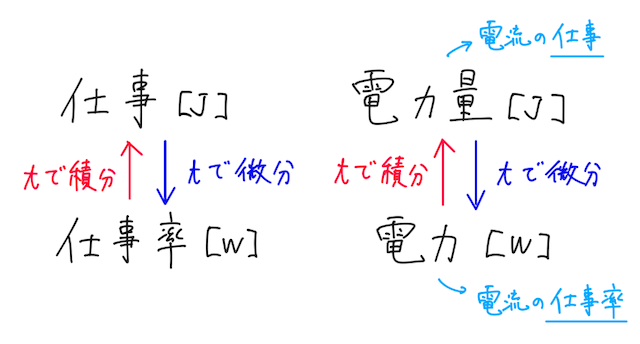
また、電力量を時間で割ったもの（時間で微分したもの）、つまり単位時間に失う位置エネルギーのことを、消費電力、もしくは単に電力という。電力は、

で求められ、単位はワット を用いる。

電力量としての と、電力の単位としての がぐちゃぐちゃになりやすいので、気をつけよう。

は仕事率の単位と同じ。電力量は電流がした仕事、電力は電流がした仕事率、と考えることができ、この対応は納得できる。

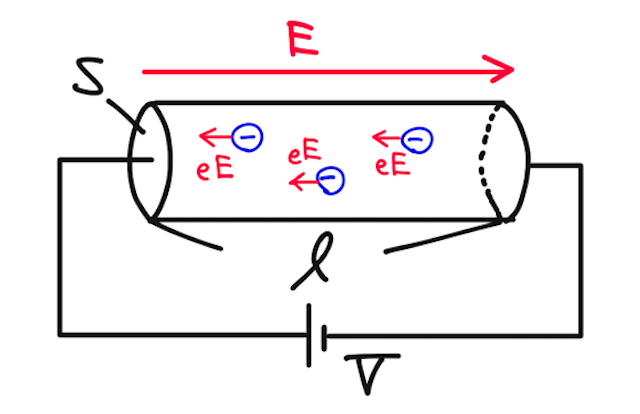
電子の運動とジュール熱

ここでは、自由電子の運動に注目して、ジュール熱を考察してみよう。

断面積 、長さ 、両端の電位差が の抵抗を考える。抵抗内の一様電場の強さを とすると、

と求められる。（詳しくは電位の辞書の一様電場中の電位差を確認）

抵抗内で自由電子の運動する速さを とすると、時間 の間に、電荷 の自由電子1個が、電場から受ける力にされる仕事 は、力×距離で、

となる。

抵抗内の単位面積あたりの自由電子の数を とすると、抵抗内に自由電子は 個あるので、全自由電子がされる仕事 は、

となり、上と同じ結果が求められる。（ただし、最後の については、電流の辞書を参照）

補足

上では抵抗について考えてきたが、これらの電力量や電力の定義

については、上で行った議論を理解していると、抵抗だけではなくコンデンサーやコイルといった素子、さらに交流回路でも、関係なく同じように考えられることが分かるので、しっかりと考え方の根本を押さえておこう。