電位
電位
電場とならび、電磁気に入ると一気に物理が難しく思う原因ランキング上位である電位について。
電位は、簡単に言ってしまえば、重力による位置エネルギーと同じように、要するに静電気力によって発生するエネルギーのこと。公式と同じくらい、定義がとても大事で、定義を押さえておくと、電磁気の他のいろんな場面で理解がしやすくなる。「あれ、どっちの電位が大きいんだっけ?」みたいなときにも、定義を理解していると瞬時にわかる。
ただ、定義を押さえるには、くぐり抜けないといけない関門がいくつかあって、まずは次の用語にピンと来ない方は、それぞれ辞書で確認してから電位を学ぼう。そっちの方が圧倒的に電磁気マスターへの近道となる。
では、電位を定義すると、電位とは、単位電荷あたりの、静電気力による位置エネルギーのこと。つまり、
で定義される。単位はボルト
基本的には、具体的な電位の公式、つまり
- 点電荷
から距離 の位置の電位は
- 一様電場
内の距離 の電位差は
を使うことになるが、もし一から電位を求める際は、定義通り、静電気力による位置エネルギーを電荷で割るか、もしくは、最初から単位電荷への静電気力を考えて、その位置エネルギーを求めれば良い。(下の公式の導出を参照)
以下、
を解説するので、興味のある方は是非。
ちなみに、動画で学んでイメージを持ちたい! という方には、受験メモ山本さんの動画や、みっきーさんの動画がオススメ。高度な知識を手に入れたい方は、ひぐまさんの動画を見てみよう。
静電気力は保存力
クーロンの法則によって導かれる静電気力(クーロン力)は、実は重力や弾性力と同じ保存力になる。つまり、静電気力のする仕事は、仕事の経路によらない。これを示すには詳しくは高度な数学が必要になるので、ここでは簡単な例として、一様電場中でサクッと確認しよう。(点電荷が作る電場中でも同様に保存力であることが示せる)
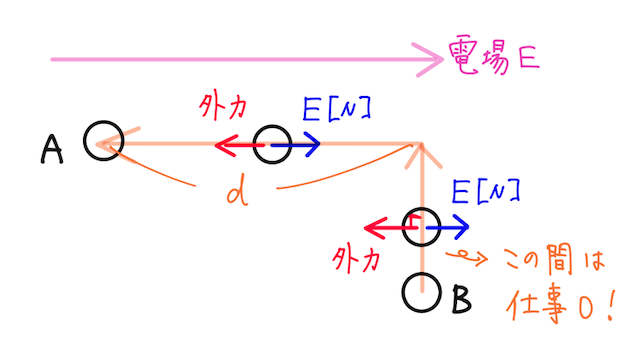
下の図のように、
経路①:A→P→B
経路②:A→B(斜めに直線移動)
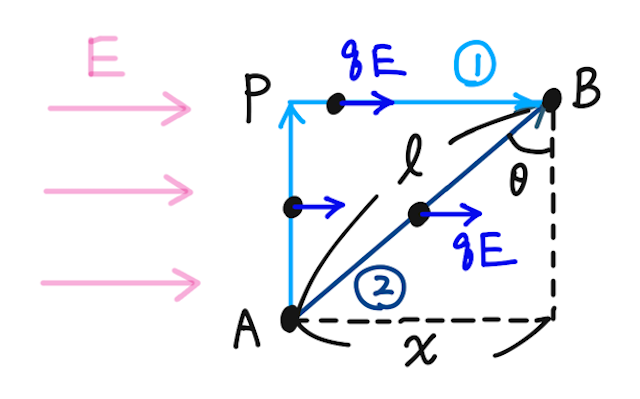
静電気力の大きさは、電場の定義より、右向きに
となる。
まず経路①について、A→Pの間で静電気力がする仕事は、静電気力の向きと変位の向きが直角なので、静電気力がする仕事は
P→Bの間では、仕事の定義より、静電気力がする仕事は、
よって、経路①において静電気力がする仕事は
と求められる。
経路②について、A→Bの間で静電気力がする仕事は、仕事の定義より
と求められる。(
よって、経路①②で静電気力がする仕事の量は等しく、またこれら以外のどんな経路を考えても仕事の量は変わらないので、静電気力は保存力である。
大事なのは、静電気力は保存力なので、静電気力による位置エネルギーを考えることができる! ということ。
以下、具体例を通じて電位の計算をやっていこう。
点電荷による電位の式
点電荷
位置エネルギーの基準点を
位置
となる。
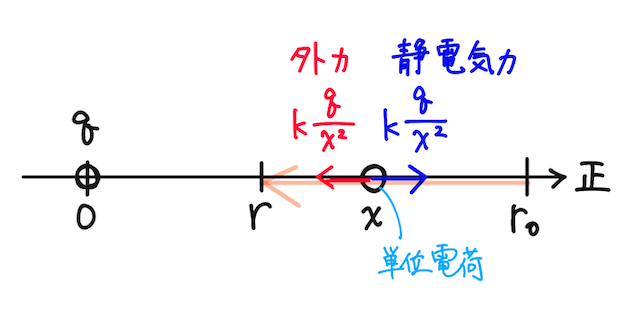
よって、電位はその定義より、
となる。(積分公式は、数学Ⅲのxのp乗の積分公式を参照)
※力が位置によって変わるため、仕事は単なる掛け算ではもとまらず、積分の出番。詳しくは仕事の辞書を参照。
点電荷による電位の式を考える際には、通常基準点を無限遠にとるので、
と求められる。
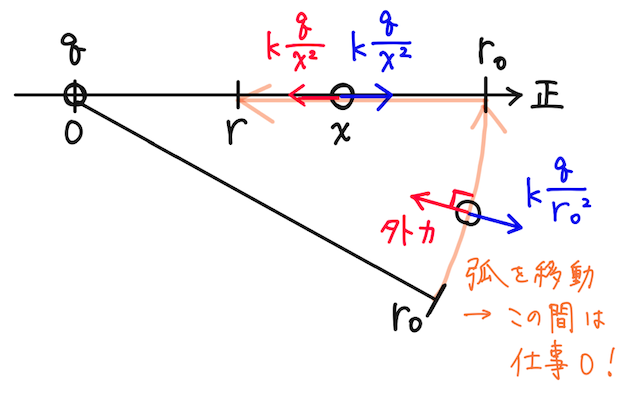
なお、平面の場合には、静電気力が保存力であることを利用して、途中で弧を描くルートをうまく選んで考えると良い。弧を移動する間は仕事が
一様電場中の電位差
強さと向きが一定の電場を一様電場という。強さ
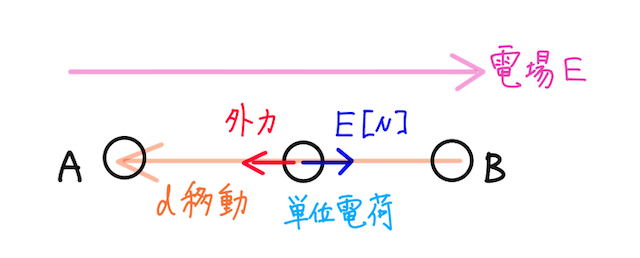
基準点をどこか適当に置くと、もちろん点
基準点を点
一様電場中の単位電荷
となる。
電位はその定義より、
と求められる。
もし
補足
ベクトル量だった電場とは異なり、電位はその定義からスカラー量なので注意しよう。つまり向きなどは存在しない。
では電位の重ね合わせはどうなるだろうか?つまり、周りに
これは、電位の定義において外力の仕事を考えるときに、それぞれの点電荷による静電気力の外力に分解して考えることができ、仕事は足し合わせられるので、それぞれによる電位を足し合わせれば良いとわかる。
この用語を含むファイル
関連動画









