終点の存在範囲
概要
平面ベクトルの最後の最後に出てくるラスボス 「終点の存在範囲」 について。最後の方なので、あまり詳しく解説されずにテストに出されることでも有名。
代表選手としては、「三角形
まず、三角形
として点
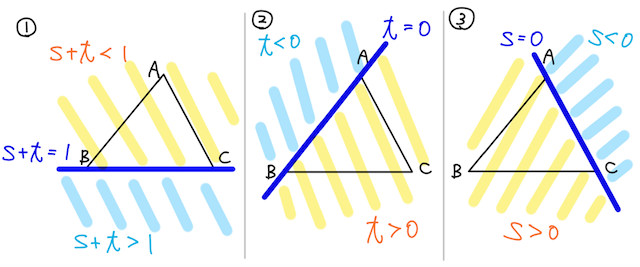
つまり、
によって、三角形の辺が作る直線に対して点
それぞれ考えてみよう。
①について
まず、点
であることは、同一直線上にある条件として常識。
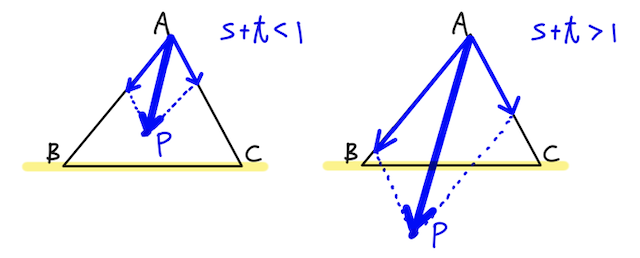
その上で、ベクトルの足し算を図形的に考えて、
- 係数同士の和が
- 係数同士の和が
というイメージは納得できるはず。手を動かして確認してみよう。
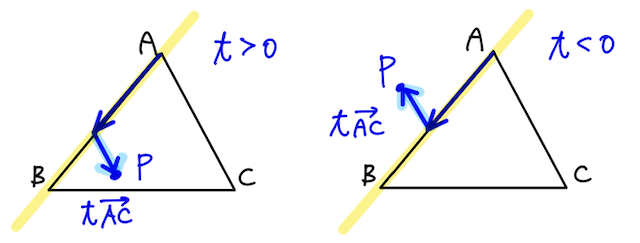
②③について
これらは同じことを言っているので、②について解説すると、まず、点
となる実数
そこに
というイメージができるはず。手を動かして確認してみよう。
基本的には、係数を独立した変数にし、上の
よく出てくる存在範囲
これまでと同じ設定
で、よく出てくる係数の条件と、対応する終点の存在範囲をまとめてみた。
上の考え方をもとに、これらについても理解してみよう。
例題
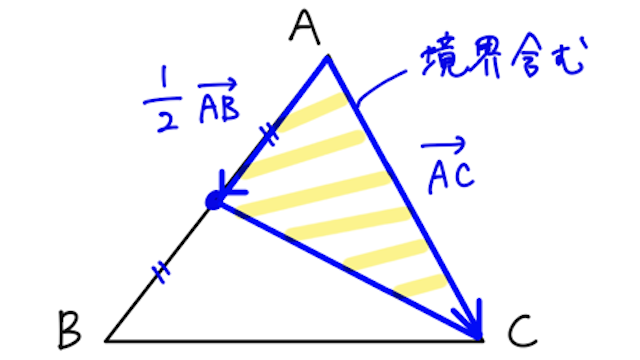
【問】実数
【答】係数をむりやり
なので、
発展
より深く理解したい方は、斜交座標を使った考え方もマスターしよう。理解すれば、こっちの方が直感的に捉えられるのでオススメ。
詳しく学びたい方は、ガチノビさんの動画を見てみよう。(導入編・基本演習編)
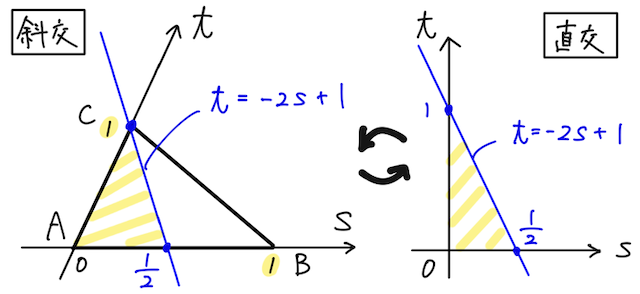
上の例題を斜交座標で捉えてみる。
まず、
がこの座標系で表す領域を考えると、下図左のように、
直交座標と比較して理解してみよう。
この用語を含むファイル
関連動画
関連用語






