共面条件
概要
点
を満たす実数
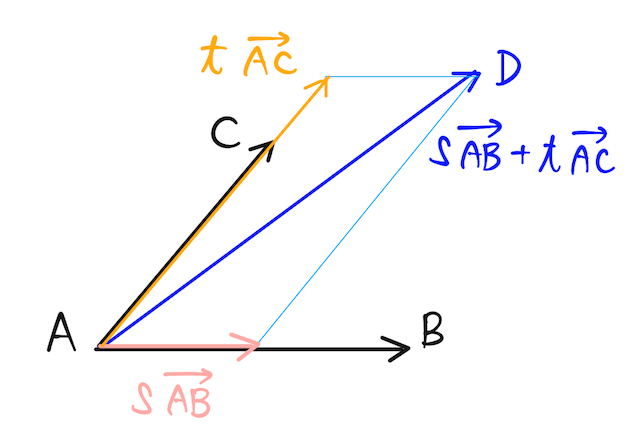
平面上のベクトルは、必ずしも
例
という
共面条件より、実数
よって、
補足
同一平面上にあると聞くと、この形の条件ではなく、 「係数の和が
「点
また細かくなるが、この共面条件を使うためには、取ってくる2つのベクトル(この場合は
「一次独立」とは、
この用語を含むファイル
関連動画
点
を満たす実数

平面上のベクトルは、必ずしも
という
共面条件より、実数
よって、
同一平面上にあると聞くと、この形の条件ではなく、 「係数の和が
「点
また細かくなるが、この共面条件を使うためには、取ってくる2つのベクトル(この場合は
「一次独立」とは、
この用語を含むファイル
関連動画