概要
点 と点 を異なる点として、点 が直線 上にあるための必要十分条件をベクトルを使って表すと、
を満たす実数 が存在すること。 点が同一直線上に乗っている条件 として、よく登場する。
が求まれば、 がどこにあるのかわかる（内分や外分の情報） 点もありがたポイントの一つ。
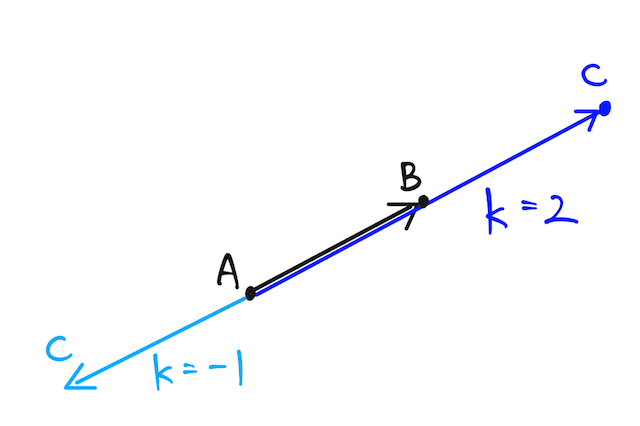
この条件は、平行条件の始点がそろっているイメージで理解できる。ベクトルの平行条件についてはこちらの辞書で確認しよう（ベクトルの平行条件の辞書）。
例
【問】
という 点が同一直線上にあるような、 を求めよ。さらに、 に対する の位置を述べよ。
【答】共線条件より、実数 を使って、次のように表せる。（ちなみに、ベクトルの成分を縦に書くと、計算間違いが減る上に、数学が得意な人に見えてカッコいい）
よって、 から 、 から と求まる。
より、
なので、図は以下のようになり、 は を に外分する。
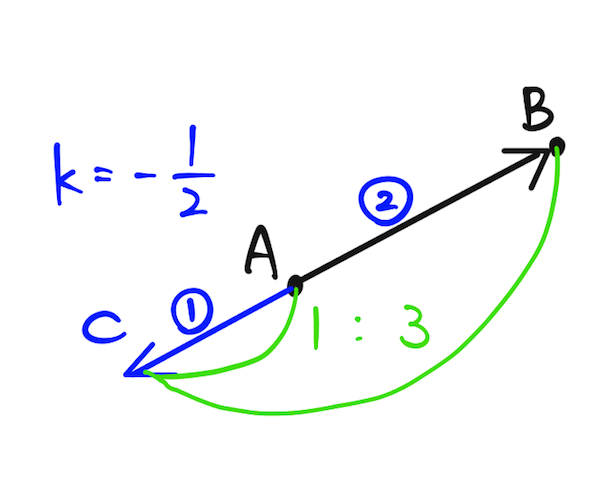
補足
必ずしも と で考える必要はなく、 と などでも成り立つので、計算しやすいように始点と終点を決めると良い。
さらに、この共線条件は空間ベクトルでも使える。
また、 つの点が一直線上にあると聞くと、この共線条件ではなく、 「係数の和が 」 という方を考える人も多いと思うが、 この つは実は同じことをやっているので、どっちかを使えばOK。
「点 が直線 上にある」
「 となる実数が存在」
「 となる実数 が存在」
「 となる実数 が存在」（これは上の共線条件と同じ）
発展（数学III）
複素数平面で、 を ではない複素数とする。複素数 について、
複素数平面での複素数の成分表示を考えれば、これも上のベクトルと同じように理解できる。（ とか とか書くと つの文字っぽいが、実数の情報を つ含んだベクトルのように考えられる）
