同一平面上にある条件

概要

点 が平面 上にあるための必要十分条件をベクトルを使って表すと、

を満たす実数 が存在すること。ただし、それぞれの点の位置ベクトルを 、、、 とおいた。

点が同一平面上に乗っている条件として、よく登場する。係数の和が であることがとても大事。

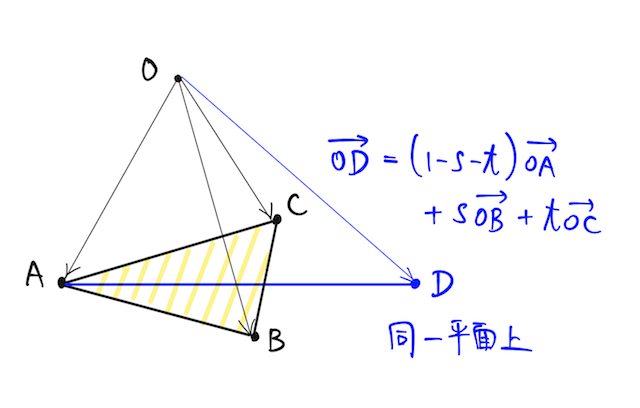
登場するベクトルは全て位置ベクトルなので、始点はどこでも良い。位置ベクトルの意味が気になって夜も眠れない方は、この位置ベクトルの辞書で復習しよう。

例

【問】

という 点によってできる平面上に、点 があるような を求めよ。

【答】基準点を原点とし、上の公式を使うと、実数 を使って、次のように表せる。（ちなみに、ベクトルの成分を縦に書くと、計算間違いが減る上に、数学が得意な人に見えてカッコいい）

よって、 を解くと 、、 から と求まる。

証明

共面条件を使って証明する。共面条件ってなんだっけ？売れてない漫才コンビ？という方はこちらの「共面条件」の辞書で確認しよう。

「点 が平面 上にある」

「 となる実数 が存在」（共面条件）

「 となる実数 が存在」

「 となる実数 が存在」

となって示される。

補足

と と は、 何が何の係数でも良い。計算が楽になるように決めるのが理想。上の例だと、成分に を含む の係数を、 という一番文字が多いものにすると、少しだけ楽ができるかと思う。