概要
点 が直線 上にあるための必要十分条件をベクトルを使って表すと、
を満たす実数 が存在すること。ただし、それぞれの点の位置ベクトルを 、、 とおいた。
点が同一直線上に乗っている条件として、よく登場する。係数の和が であることがとても大事。 がわかれば、 がどこにあるかもわかる。
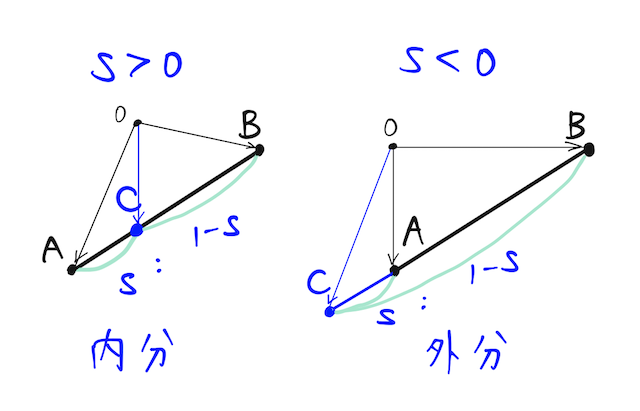
(なぜ というように係数の逆になるかは、分点公式の辞書を参照。)
登場するベクトルは全て位置ベクトルなので、始点はどこでも良い。位置ベクトルの意味が気になって夜も眠れない方は、こちらのこの位置ベクトルの辞書で復習しよう。
例
【問】
という 点が同一直線上にあるような、 を求めよ。さらに、 に対する の位置を述べよ。
【答】基準点を原点とし、上の公式を使うと、実数 を使って、次のように表せる。(ちなみに、ベクトルの成分を縦に書くと、計算間違いが減る上に、数学が得意な人に見えてカッコいい)
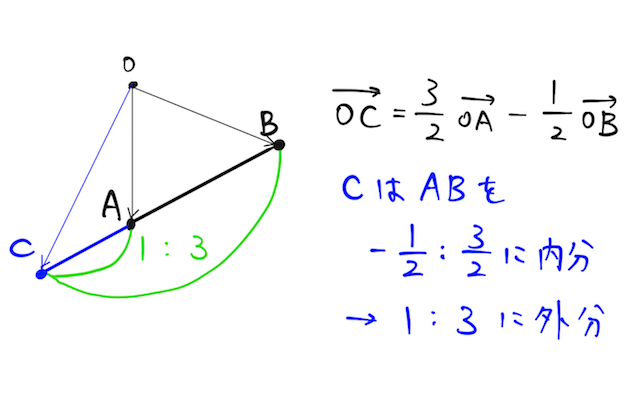
よって、 から 、 から と求まる。
より、
なので、図は以下のようになり、 は を に外分する。(係数から比を求める方法がわからない方は、こちらの分点公式の辞書を参照。)
証明
共線条件を使って証明する。共線条件ってなんだっけ?という方は共線条件の辞書で確認しよう。
「点 が直線 上にある」
「 となる実数 が存在」(共線条件)
「 となる実数 が存在」
「 となる実数 が存在」
となって示される。
補足
と は、 どっちがどっちの係数でも良い。
あと、空間ベクトルでも成り立つ。









