合成関数の微分

概要

数学IIIの微分の分野で、めちゃめちゃよく使うのが、この 「合成関数の微分」 と言われる式。

つまり、関数の中に何かしらの の式が入っているときに、その式をまるごと文字と見て、その文字で微分し、その固まりの での微分を最後にかけるという式。

これは公式を文字で覚えても全く使えないので、例と図で確認して、寝ながらでもできるようになろう。

例

詳しくは、

少しレベルを上げよう。

詳しくは、

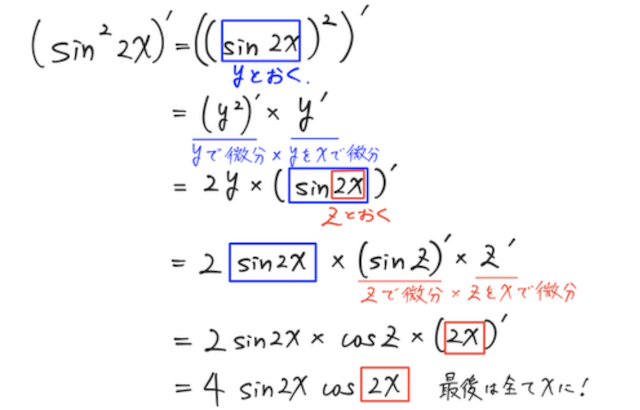
証明

導関数の定義から考える。

となり示される。

（この証明では、 を暗に仮定している。こういう仮定の存在しないカッチリとした証明については、例えばこちらの式変形チャンネルさんの動画をチェック。）

補足

関数が何重にもなっているときは、例でわかる通り、 より外側にある固まりからまとめていくのが良い作戦。