## 概要

任意の角 $\alpha, \beta$ に対して以下の公式が成り立つことが加法定理として知られている。

$$
\begin{align} 
\sin(\alpha+\beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta\\\\
\sin(\alpha-\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta\\\\
\cos(\alpha+\beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta\\\\
\cos(\alpha-\beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta
\end{align} 
$$

上の式を用いると、$\tan$ の加法定理も求めることができ、

$$
\begin{align} 
\tan(\alpha+\beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}\\\\
\tan(\alpha-\beta) = \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha\tan\beta}
\end{align} 
$$

となる。覚え方については、コスモスが咲く可愛いらしいものから、ど下ネタまで色々あるので、ググって自分に合うものを探そう。

※ $\tan$ の加法定理の導出方法（これは覚えてなくても導ければOK）

$$
\begin{align} 
\tan(\alpha+\beta) &= \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\\\
&= \frac{\sin\alpha\cos\beta + \cos\alpha\sin\beta}{\cos\alpha\cos\beta - \sin\alpha\sin\beta}\\\\
&= \frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta} + \frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta} - \frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\\\
&= \frac{\frac{\sin\alpha\cancel{\cos\beta}}{\cos\alpha\cancel{\cos\beta}} + \frac{\cancel{\cos\alpha}\sin\beta}{\cancel{\cos\alpha}\cos\beta}}{\frac{\cancel{\cos\alpha\cos\beta}}{\cancel{\cos\alpha\cos\beta}} - \frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\\\
&= \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}
\end{align} 
$$

のように、$\tan=\displaystyle\frac{\sin}{\cos}$ の相互関係を使いつつ、$\cos\alpha\cos\beta$ で分母分子を割って導くのがポイント！

## 例

$$
\begin{align} 
\cos 165^{\circ}&=\cos (120^{\circ}+45^{\circ})\\\\
&=\cos 120^{\circ}\cos 45^{\circ}-\sin120^{\circ}\sin 45^{\circ}\\\\
&=-\frac{1}{2}\cdot\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}\\\\
&=-\frac{\sqrt{2}+\sqrt{6}}{4}
\end{align}
$$

## 証明

ここでは、$\sin$ と $\cos$ の加法定理を証明する。

※ 結構アクロバティックな証明なので、動画でわかりやすく学びたい！という方は、以下の動画を参照しよう。
- [古賀真輝さんの証明動画](https://okedou.app/videos/hPF158zkFD8)（背景知識の証明も）
- [ガチノビさんの証明動画](https://okedou.app/videos/AJ8sIz9TSLY)（ハイレベルな証明方法も）
- [林俊介さんの証明動画](https://okedou.app/videos/48EgUJVoKCw)（簡潔）

■ まず、単位円上で、角 $\alpha$ の動径 $OA$、角 $\beta$ の動径 $OB$ をとる。動径は、原点を中心としてクルクル回る線だと思っておこう。

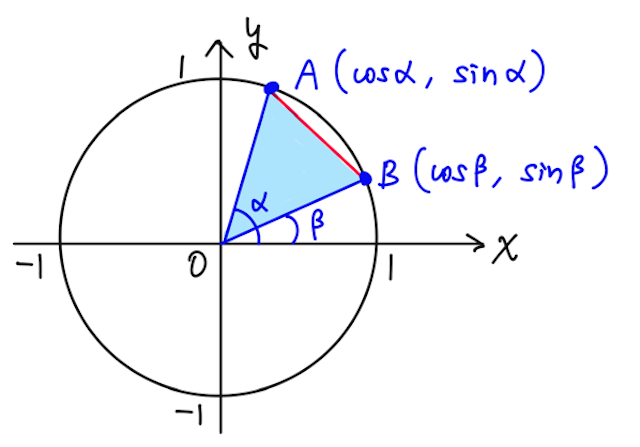
![Untitled 1 P1.png](https://oke-files.s3.amazonaws.com/uploads/RYUQSD9bD1bIi/4f6f92f000a94e38b2204b16023f2e2c.png)

このとき、$A$ と $B$ の間の距離について、[2点間の距離の公式](https://dic.okedou.app/words/p/8FmJKYZqppuUk)から、

$$
\begin{align}
AB^2=&(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2\\\\
=&(\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta)\\\\
&+(\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta)\\\\
=&2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\cdots(1)
\end{align} 
$$

と表せる。ただし、角度が同じであれば $\sin^2+\cos^2=1$ が成り立つという[三角関数の性質](https://dic.okedou.app/words/p/068nD9NIopdXh)を使った。

一方、**$\triangle OAB$ を原点周りに $-\beta$ だけ回転させて、$\triangle OA'B'$ を作ってみる。**

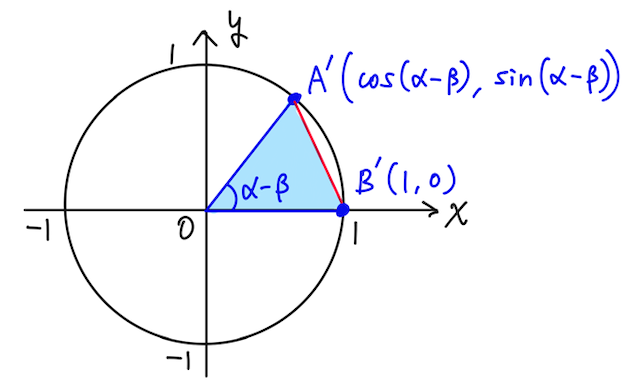
![Untitled 1 P2.png](https://oke-files.s3.amazonaws.com/uploads/RYUQSD9bD1bIi/d22819207d0344419f24f470f8ebff0f.png)

そうすると、点 $A'$ や点 $B'$ の座標は上のようになり、この2点の間の距離について考えると、同じく[2点間の距離の公式](https://dic.okedou.app/words/p/8FmJKYZqppuUk)から、

$$
\begin{align}
A'B'^2=&(\cos(\alpha-\beta)-1)^2+(\sin(\alpha-\beta)-0)^2\\\\
=&(\cos^2(\alpha-\beta)-2\cos(\alpha-\beta)+1)\\\\
&+\sin^2(\alpha-\beta)\\\\
=&2-2\cos(\alpha-\beta)\cdots(2)
\end{align} 
$$

が得られる。

ここでよくよく考えてみると、$\triangle OAB$ と $\triangle OA'B'$ はただ回転させただけなので、もちろん $AB$ と $A'B'$ の長さは等しいはずである。

よって、$(1)(2)$ より、

$$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\cdots(3)$$

が成り立つ。これで、**$\cos$ の引き算バージョンの式**の証明が完了。

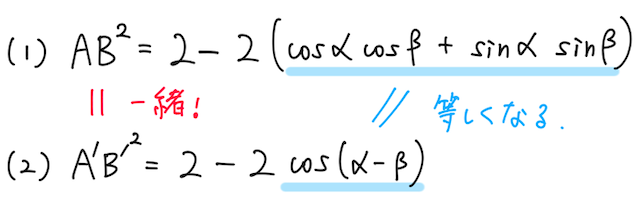
![Untitled 1 P1.png](https://oke-files.s3.amazonaws.com/uploads/RYUQSD9bD1bIi/63efd835e7474fcb8521cdb6239ff35e.png)

■ $(3)$ の $\beta$ に $-\beta$ を代入すると、

$$\cos(\alpha+\beta)=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)$$

となって、

$$
\begin{align}
\cos(-\beta)&=\cos\beta\\\\
\sin(-\beta)&=-\sin\beta
\end{align}
$$

であることを用いると（この性質については、[こちらの辞書](https://dic.okedou.app/words/p/y7gwz9AuY0uWu)を確認）、

$$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\cdots(4)$$

となり、**$\cos$ の足し算バージョンの式**を示すことができる。

■ また、$(4)$ の $\alpha$ に $\displaystyle\frac{\pi}{2}-\alpha$ を代入すると、

$$\scriptsize\cos\left(\frac{\pi}{2}-\alpha+\beta\right)=\cos\left(\frac{\pi}{2}-\alpha\right)\cos\beta-\sin\left(\frac{\pi}{2}-\alpha\right)\sin\beta$$

となって、

$$
\begin{align}
\small\cos\left(\frac{\pi}{2}-\alpha+\beta\right)&=\small\cos\left(\frac{\pi}{2}-(\alpha-\beta)\right)=\sin(\alpha-\beta)\\\\
\cos\left(\frac{\pi}{2}-\alpha\right)&=\sin\alpha\\\\
\sin\left(\frac{\pi}{2}-\alpha\right)&=\cos\alpha
\end{align}
$$

であることを用いると（この性質については、[こちらの辞書](https://dic.okedou.app/words/p/y7gwz9AuY0uWu)を確認）、

$$\sin(\alpha-\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta\cdots(5)$$

となり、**$\sin$ の引き算バージョンの式**を示すことができる。

■ そしてさらにこの $(5)$ の $\beta$ に $-\beta$ を代入すると、

$$\sin(\alpha+\beta) = \sin\alpha\cos(-\beta) - \cos\alpha\sin(-\beta)$$

となって、上と同様に

$$
\begin{align}
\cos(-\beta)&=\cos\beta\\\\
\sin(-\beta)&=-\sin\beta
\end{align}
$$

を用いることで、

$$\sin(\alpha+\beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$$

となって、**$\sin$ の足し算バージョンの式**を示すことができる。これでめでたく全て示される。

### 補足

- 加法定理の証明は、1999年に東京大学の入試問題となったことでも有名
- 符号がわからなくなったときは、例えば $\alpha=60^{\circ},\beta=30^{\circ}$ などの値が**わかる数を代入し、合っているか確認**することができる

加法定理

概要

例

証明

補足

タグ