合成

概要

三角関数の和

を、以下のように変形することを三角関数の合成と呼ぶ（ ではないとする）。

最後は加法定理を使っている。途中でいきなり新しい角度 が出てきてギョッとするが、これは、

を満たす角で、このような は にただ つ存在 する。

を図形的に示すと、以下の通りとなる。

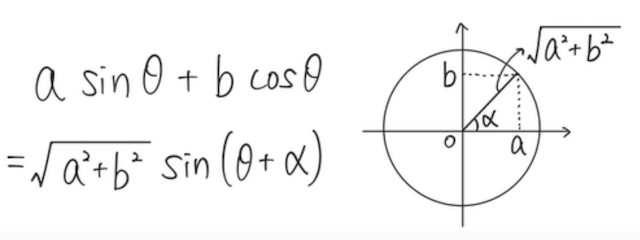
この新しい角度を作ったことによって、 の式と の式を、一つにまとめることができた。

例

【問】 の範囲で、以下の方程式を解け。

【答】 と の中身が同じなので、合成によって左辺を1つにまとめることができる。（符号がマイナスでも、全く同じように加法定理で考えればOK）

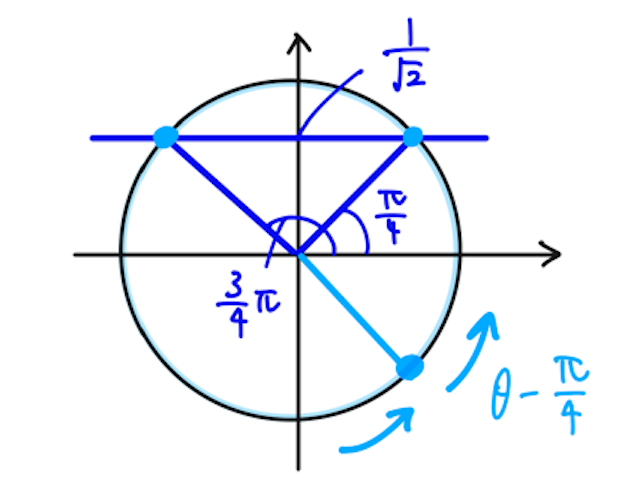
よって方程式は

となる。ここで、角度の範囲は

より、

と求まる。（ゴールはあくまでも を求めるということに注意！！）

補足

これはとても大事な変形で、補足もたっぷりある。

• 覚えなくても、上の式変形のように作れればOK
• 実際に合成するときは、上のように変形を行なっていき、 と から を自分で求める
• 有名角として が求められない場合は、 のまま置いておく
• と のどちらかからだけだと、基本的には は一つに決まらないので、 必ずどちらも使って、単位円上で を決定するようにしよう
• 最初の と の中身の角度（）が違うと使えないので注意
• 上の例題のように、合成することにより式の項数を減らすことができるので、方程式や不等式を解くのがとても楽になる
• ちなみに、以下のように角度の取り方を変えると で合成することもできる。

ただし、 は

を満たす角で、このような も にただ つ存在 する。（図形を考えれば、 が成り立つこともわかる！）