三角形の面積
概要
で計算できる。道ゆく人に、三角形の面積公式は?と聞いたら、ほとんどの人は「底辺×高さ÷2」と答えると思うが、高校数学では、 2つの辺とそのなす角の
ちょっと大人になった気分。
また、数学Bのベクトルの範囲になるが、
を使っても計算できる。さらに、
とおくと、成分で計算することもできて、
となる。
証明(ベクトルじゃない方)
三角形の面積公式
を示す。頂角の大きさによって図が変わってくるので、以下、
【 i 】
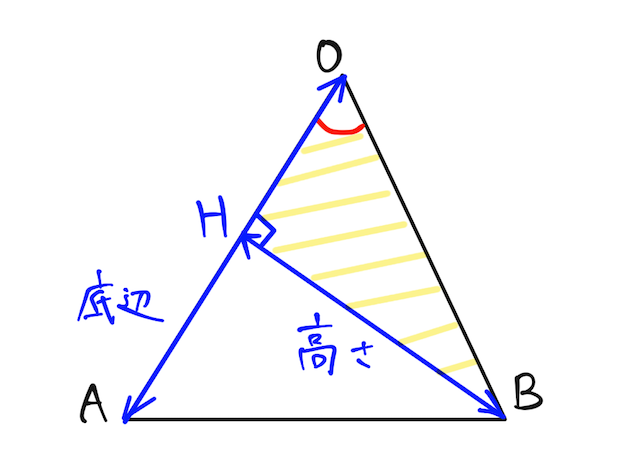
高さ
と求められるので、三角形の面積は
となり
【 ii 】
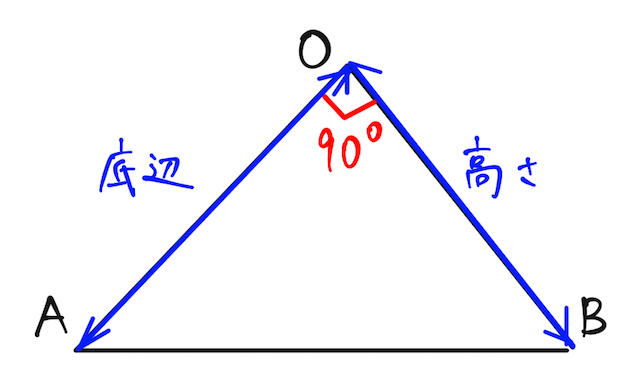
となり
【 iii 】
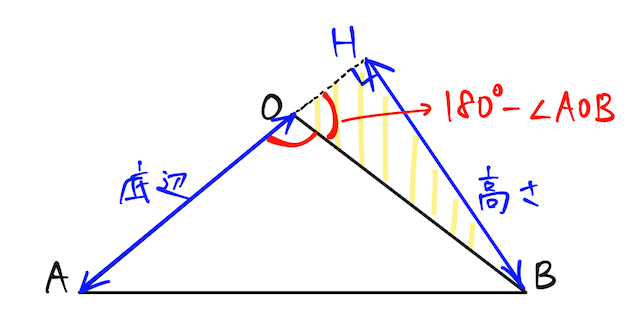
高さ
と求められるので、三角形の面積は
となり
以上【 i〜iii 】で証明完了。
証明(ベクトルの方)
上で示した三角形の面積公式
を使って、示していく。ここでは三角形が存在しているとして、
で考える。
となって、示したかった式
補足
- 面積を求めたい三角形の1つの頂点を基準点として、残りの2点の位置ベクトルを求めると、このベクトルの公式が使える(上では基準点をOとして考えているが、原点である必要はない)
- 成分表記の内積を使ったうまい証明は、ガチでノビる受験数学のシーナさんの動画を参照。
- ベクトルでの表記は空間ベクトルでも成り立つが、成分表記は平面ベクトルのみで成立。これは勘違いしやすいので注意を!
- 成分表記はよく忘れてしまう。記憶が曖昧なときは、 わかりやすい簡単な図形、例えば下の
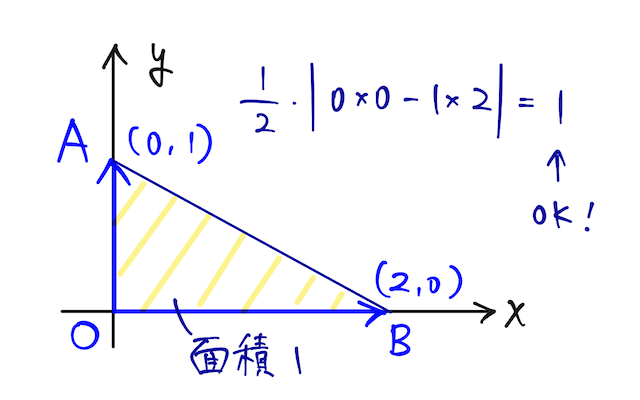
関連動画







