位置ベクトル

概要

とある点を基準点としてとり、そこから伸びるベクトルを考える。例えば点 へ引かれたベクトルを、点 の位置ベクトルと呼ぶ。

ベクトルで迷子になる原因の多くは、この「位置ベクトル」という最初の関門にある。第 ステージにクッパがいるようなもの。

なぜこんなものを考えるかというと、例えば 「ベクトルが の点です」 と言われても、平面上でその点の位置を定めることはできない。

でも、「 を基準点としたベクトルが、 の点です」 と言われると、座標平面上で、「あ〜、点 だな」とすぐにわかる。

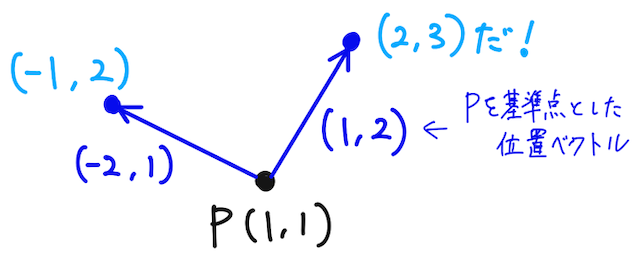
つまり、基準点からの位置ベクトルを考えてあげることで、座標上の点とベクトルが対応することになり、 点の位置をベクトルで定めることができるようになるのが、この「位置」ベクトルを考える理由。

基準点は自由に取れるが、原点 を基準点として考える場合が多いし、何より理解しやすいので、わからなければ原点を基準点として考えてみよう。

原点からの位置ベクトルを考えると、位置ベクトルの成分表示がその点の座標と等しくなることが、下の図からもわかる。

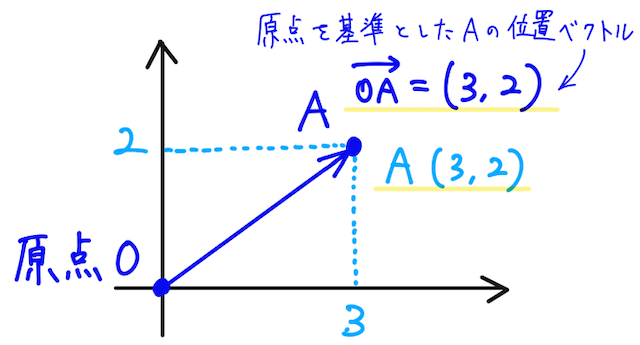
点の位置を位置ベクトルで定めることができるイメージが、理解できると思う。

なお、普通のベクトル を位置ベクトルに直すには、 と、基準点を始点にしてそろえてあげれば良い。

補足

• 位置ベクトルは、全て同じ基準点からのベクトルなので、 基準点は省略されることがある
• 例えばを基準点としたとき、 を 、 を と小文字を使って表されることも多い（小文字が使ってあったら、基本的に位置ベクトル）
• 空間ベクトルでも同様