x分のsinxの極限

概要

数学IIIで三角関数の極限が出てきたらこれ、というくらい定番の人気者。消しゴムのMONOのようなモノ。ダジャレではない。

大事なのは、 分母の文字と分子の の中身の文字が等しいときに、この式が成り立つということ。下の例でも確認しよう。

例

【問】以下の値を求めよ。

【答】変形しまくって を発掘してあげて、上の形が使えるところに持っていく。

なお、初めの分子を半角の公式で変形しても解ける。

証明

これは知っていないとなかなか証明できない。概略は以下の通り。

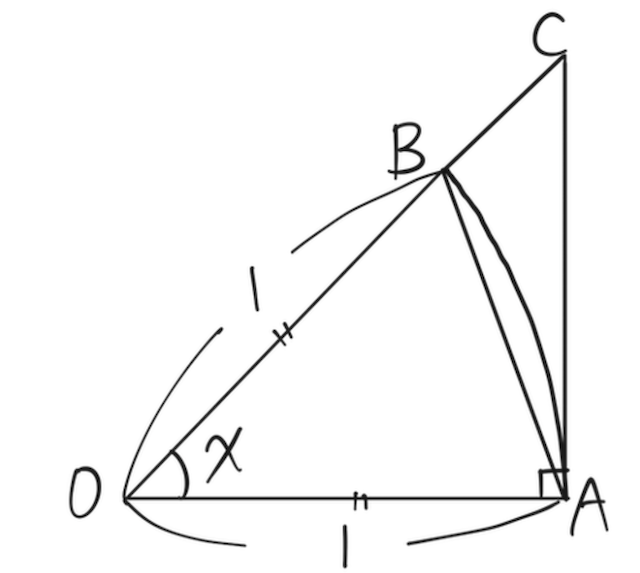
上の図のように、半径が で中心角が の扇型 に対して、2つの三角形 と を作る（ は十分に に近い正の数とおく ）。

これらの面積の関係は、

なので、それを式にすると、

全ての辺を で割って、整理すると、

ここで、

なので、はさみうちの原理（辞書はこちら）により、

が示される。この式に を代入して変形すると、

も示される。よって極限は となる。

補足

• 三角比で以外が出てきたら、三角比の公式をフル活用して を引っ張り出す 。
• という極限ではない場合（無限大に飛んでいったり）には、置換してこの形に持っていく。
• がマイナスの時は、置換すれば上と同様に示せる。例えば、こちらの福田次郎さんの証明動画を参照しよう。