垂心のベクトル

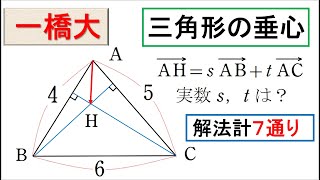
＜問題＞ 平面上に △ABC があり，AB= 1，AC = 2， ∠ BAC = 45◦ であるとする.△ABC の垂心を H とするとき，ベクトルAH を ベクトルAB，ベクトルAC で表せ． 3つの解法を紹介します。複数のアプローチを考えることは、理解を深めることにつながります。 ＜この問題について＞ 条件を立てた後は単純作業，というのがベクトルの強みです． AH=の式は自分で別に立てる必要あり，という点だけ注意が必要です． そう考えると解法3は少し不思議な解答ですね． シリーズ「ベクトルに捧げる，2020夏。」も今日で6日目．あと27日． まだまだ始まったばかりです．今日から4連休ですね． ＜目次＞ 00:00 問題説明 00:20 解1 内積による垂直条件 03:04 解2 正射影ベクトル 04:47 正しい図 05:34 解3 メネラウスの定理 07:10 まとめ ＜キーワード＞ #垂心 #垂線の交点 #垂直条件 #平面上にある条件 #正射影 #メネラウスの定理 #外分点 ＜はやくち解説とは＞ かったるい説明に嫌気がさしたときに見る動画。早口×早送りで解説しました。雰囲気を掴んでもらえたらいいと思っています。 ＜使用機材＞ カメラ：iPhone 11 Pro タブレット：iPad Pro 12.9インチ アプリ：Good Notes 5 編集ソフト：Final Cut Pro