メネラウスの定理

概要

下の三角形 と直線 に対して、次の等式が成り立つことをメネラウスの定理という。

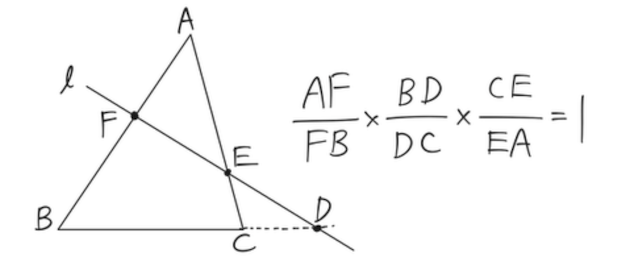
どの点から始めてもいいので、三角形の頂点と直線上の点を交互に通りながら、一筆書きして元の点に戻ってくるイメージを持とう。

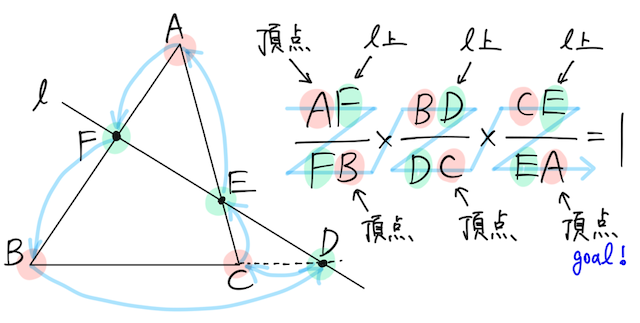
証明

下の図の通り、点 から直線 と平行な直線を引き、辺 との交点を とする。このとき、平行線と線分比の関係から、

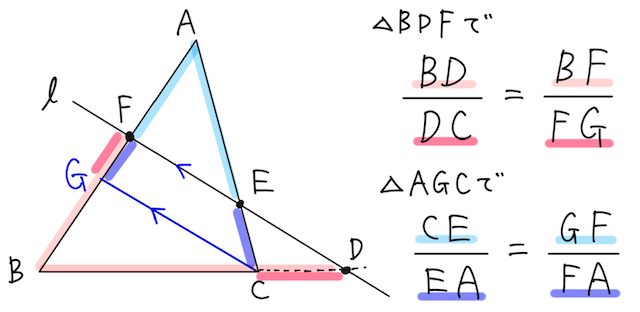
が成り立つので、

となって示される。（全部打ち消しあう！）

例

【問】下の図において、 を求めよ。

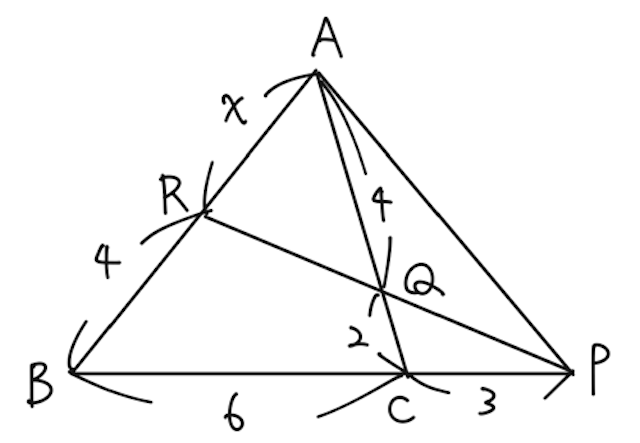
【答】

と直線 に関して、メネラウスの定理から、

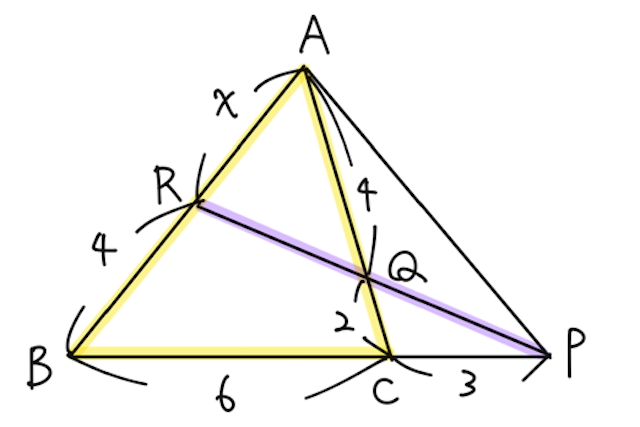
これを解いて、

と求められる。

ちなみに、 と直線 に関してメネラウスの定理を使っても式を作ることができるので、興味のある方は考えてみよう。

補足

• 覚え方は、 三角形の一つの頂点からの一筆書きで覚えるのが王道（全ての点を通っていく）
• 三角形と一本の直線について考える時に、使えることが多い
• チェバの定理と間違えやすいが、チェバは三角形と一つの点に対して使う
• ちなみに、メネラウスは 世紀の人で、チェバさんは 世紀の人。チェバさんがメネラウスの定理も再発見して、公表した。
• 使い方については、ヨビノリさんの「チェバの定理とメネラウスの定理の本質」の動画も見てみよう！
• 逆も成り立つ。つまり、任意の三角形 において、辺 、、 またはその延長上にそれぞれ 、、 があり、このうち 個あるいは 個の点が 辺の延長上にある（辺上に無い）ときに、以下の式が成り立つのならば 点 ・・ は 直線上にある。