お初にお目にかかります、ぱたです。
今回は円周率 π の近似値を計算する方法とその歴史を、大学入試の過去問をベースに紹介していきます。
この記事を最後まで読んだ人は、すっかり円周率評価マスターになっているかも...?
無論、そんなものになる必要性は全くありませんが...笑
円周率評価の歴史(前編)
現代ではすっかり「数学で習う有名定数ランキング」n年連続1位として国民に定着している円周率。(?)
その値や性質は決して「天から降ってきた」ものではなく、歴年の数学者たちが様々な方法で得てきたものなのです。
この記事では、そのユニークな方法たちを年代順に紹介していきたいと思います。
東大の有名問題 (2003 理系第6問)
円周率評価の歴史に入る前に、かつて受験数学界に衝撃を与えた伝説の入試問題を紹介しておきます。
今となっては有名な問題です。当時はゆとり教育によって円周率は3.14ではなく3として計算するという恐ろしい風潮がありました。
無論、このような超大ざっぱな近似をしてしまえば数学的な矛盾が死ぬほど出てくるので数学教育としてまずいわけです。
この問題の背景に東大によるゆとり教育への警鐘を感じ、受験数学マニアとしては大変エモいです(?)
実はこの年、大阪大学もゆとり教育に対する警鐘を鳴らしているとくみ取れるような出題がありました。円周率が無理数であることの証明です。
要は
「円周率って無理数なんだよ、絶対に円周率を3として計算させるなんてことしないでね ^^) 」
ということを言いたかったのでしょう。
円に内接・外接する正多角形による円周率評価の時代

最初に「円周率は3.14くらい」というレベルまで評価したのは古代ギリシャの数学者・アルキメデス(紀元前287~212年)です。
彼は、円周とその円に内接・外接する正96角形の周の長さの大小関係を用いて円周率を評価しました。
(歴史的に最初にこの方法を思いついたのは紀元前2000年頃だそうですが、調べた限りでは発見者の名前も不明だったり不確定な部分が多いので省きました。)
図より明らかですが、この正n角形を用いた近似はnの値が大きくなればなるほど正確な値が得られます。
例えば上記の東大の問題はこの方法で解くことができて、最短で正八角形を用いて近似すれば円周率が3.05より大きいことを示すことができます。(ちなみにアルキメデスが用いた正九十六角形で計算すると、3.14084 < π < 3.14286 くらいまで得られます。)
「3.05より大きい」という値の設定とこの方法がいたって自然な円周率の近似の仕方であることから、東大側はこのような解法を主に想定していたと考えられます。
この評価方法、全世界の有名な数学者が行っているのですが、その中でも特に変態的なのはドイツの数学者・ルドルフによる評価です。
彼は1610年に亡くなるまでの間になんと正262角形 (=約461京)を用いてπの小数第35位までを正しく評価しました。
この(狂気の)功績が讃えられ、かつてドイツでは円周率のことをルドルフ数と呼んでいたそうです。
現在、再建版ではありますが彼の墓石が残っています。
この方法は、当時最先端の数学研究がなされていたインドでも1400年頃まで続きます。
参考: 鈴木貫太郎さんの、円周率が3.05より大きいことの証明動画
インドの天才数学者による円周率評価(2020 お茶の水女子大学 第6問)

昨年、お茶の水女子大学の入試問題でこんな問題が出題されました。
(ちなみに、お茶の水女子大学の数学は難問揃いですが興味深い話題を取り扱っている良問ばかりなので最難関大学対策の演習におススメです。)
誘導がある分、先ほど紹介した東大の問題より厳しい評価が求められていることが分かります。
じつはこの問題にも歴史的な背景があります。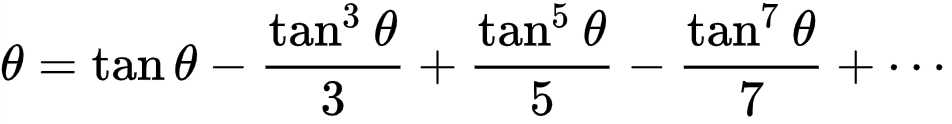
1300~1400年ごろ、インドの数学者・マータヴァが三角関数と逆三角関数のマクローリン展開を発見しました。
この式はヨーロッパでも1670年ごろにライプニッツによって発見されます。当時のインドの数学がどれだけ時代の最先端だったかがよくわかる事実ですね。
その中でも、上に示したtanθの逆関数のマクローリン展開にθ=π/6を代入して、円周率を小数第10位まで正しく評価しました。(諸説あり)
これは当時の世界記録を更新するレベルの厳密さでした。
お茶の水女子大学の問題の(4)に登場する式は、この式の右辺の第2項までを用いた近似式が題材となっています。
高々第2項までの近似で円周率が3.11より大きいことを示せることから、正多角形による近似よりはるかに効率がよいことがうかがえます。
次回予告
えーここで入試問題とともに円周率評価の歴史を振り返っている途中ですが、長くなりそうなので残りは後編に回します。
👉 「大学入試からみる円周率の歴史 【数学者たちの努力の結晶】後編」を見る
後編では積分による円周率評価、そして現代におけるコンピューターによる円周率評価について紹介していきたいと思っております。
それではまたこんど!




