概要
母集団全体の中で、ある性質 をもつ割合を とする(例えば、日本の人口のうち 以上の人の割合、みたいなイメージ)。この のことを、母比率という。
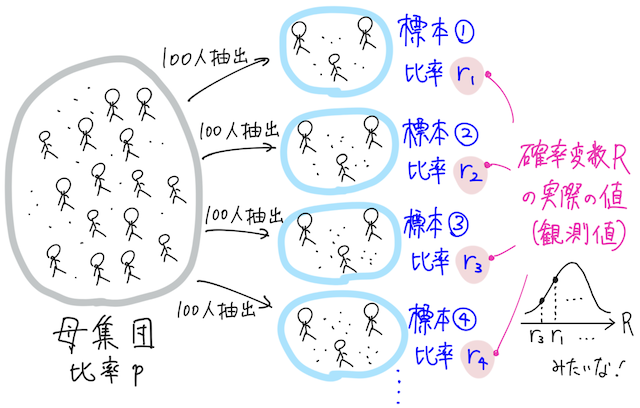
母集団から、無作為(ランダム)に大きさ の標本を抽出するとする。(「標本」はとりあえずデータのことだと思っておけばよく、要するに、母集団全体から 個のデータを選ぶということ)
このとき、抽出された標本 のうち、性質 をもつ割合のことを標本比率という。標本の比率なので、そのままのネーミング。
この標本比率( とおく)は、選ばれる標本によって変化するので、標本を何個も作ると、基本的には標本比率の実際の値はそれぞれ変わる。
日本中で 人ずつ集めて 以上の人の割合を調べると、どの 人を集めるかで比率は変わってくるよね、っていうこと。
つまり、標本比率は確率変数であり、標本比率の確率分布というものを考えられる。
確率変数としての標本比率 と、実際にとってきた標本での比率(標本比率の観測値) の区別がとてもこんがらがりやすいので、注意しよう!
このとき、母比率を 、標本の大きさを とすると、標本比率 の期待値と分散は、母集団の値を用いて、
となる。この分散の値より、標準偏差は
と求められる。
理由が大事なので、下の詳細も一緒に確認しておこう!
詳細
母集団の中で、性質 を持つものの割合(母比率)を とする。そこから標本として無作為に 個選び、その中で性質 を持っているものの数を とする。
このとき、 の確率分布は二項分布 である。これは二項分布の定義そのもの!
よって、確率変数 の期待値と分散は
となる。
ここで、 個の標本の中で、性質 を持っているものの割合(標本比率)は と求められるので、これを とおいて、確率変数 の確率分布を考えると、確率変数の変換の性質から、
とわかる。
※ それぞれ係数倍を外に出すときの性質を思い出そう!
また、二項分布 に従う確率変数 は、 が十分に大きいとき、正規分布 に従うとみなせる。これはとても重要な性質なので、忘れている人は二項分布の用語ページで確実に復習しておこう。
このとき、 は のとりうる値をそれぞれ 倍しているだけなので、 も正規分布つまり、 に従うとみなせる。つまり、標準化すると、
で定められる確率変数 は標準正規分布に従うとみなせることになり、さまざまな確率を求めていくことができる。
補足
なぜこんな「標本比率」というものをわざわざ考えるのだろうか?
これは、標本平均と同じように、母集団の母比率がどのようなものかわからないときに威力を発揮する。
詳しくは「母比率の推定」という用語ページ(全力で作成中)で解説するが、母比率がわからない状況であっても、たくさんの標本をとってきて、標本比率の値を求めることはできる。
標本が十分大きいと、標本比率の分布は正規分布とみなせるので、標本比率の実際の観測値や、その正規分布の形を使って、だいたい母比率がどのくらいか推定することができるのである。
これが母比率を考えることの醍醐味の一つで、母集団の状況がはっきりわかることの方が少ない実社会でも数多く応用されている。例えば、冒頭に挙げたように、「日本の人口のうち 以上の人の割合」を調べようと思いついても、全国に行き、 人ずつ身長を聞いていくことはほぼ不可能だが、ある程度多くの標本をとって標本比率というものを考えることで、日本全体についてのだいたいの比率がわかるというのがすごいところ!








