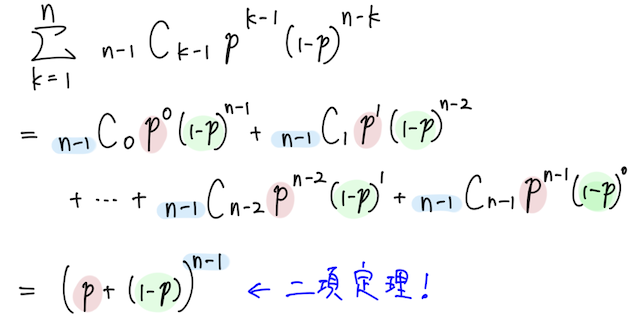概要
ある試行で事象 の起こる確率が であるとき、この試行を 回行って の起こる回数を とおくと、()という値をとる確率は
となる。(つまり 回中 回 が起こる確率であり、反復試行の確率を思い出そう)
確率分布がこのように表されるとき、この分布を二項分布と呼び、 で表す。
二項分布の期待値と分散は、この と からすぐに求めることができ、
となる。また、標準偏差は、分散から
となる。
さらに、重要な性質として、二項分布 に従う確率変数 は、 が十分に大きいとき、正規分布 に従うとみなせる。詳しくは下のセクションで扱う。
期待値と分散の証明(泥臭くver)
では、二項分布 に従う確率変数 の期待値と分散の式を、定義から泥臭く求めてみよう。
まずは期待値について。とりうる値と、その値をとる確率を掛けて足していけばOK!
確率変数 のとりうる値は 〜 の 種類であり、 をとる確率 は二項分布の定義から
であるので、 の期待値は、定義より
と求められる。
については、下の二項係数についての公式を用いた。(成り立つ理由はリンク先の用語ページをチェック)
については、二項定理の形を見抜いて、あえて を つ前に出している。
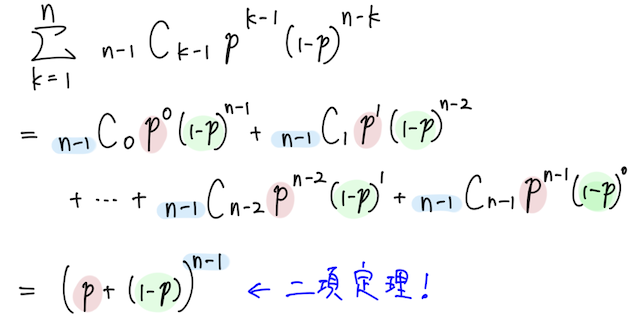
では 分散について。
定義通り計算しても、「確率変数の 乗の期待値」-「期待値の 乗」のやり方で求めても、大して労力は変わらない。ここでは後者でやってみよう。
そのためにまず、確率変数 の期待値を求める。とる値が 乗になっていき、それぞれの値をとる確率はそのままなので、定義より
となる。
については、期待値の定義式を分けつつ、その後の変形をやりやすくするために とあえて分けて計算している!
については、期待値のときと同様、下のように二項係数についての公式を 回連続で用いている。 のときはシグマの中の値が になるので除いている( を残してしまうと、添字の がおかしくなる)。
※ 個目の式は添字を つ下げただけ。
については、二項定理の形を見抜いて、あえて を前に出している。
よって、求める の分散は
と求められる。
期待値と分散の証明(上手にver)
二項分布に従う確率変数 について、見方を変えてみよう。
確率変数 は、ある試行で事象 の起こる確率が であるとき、この試行を 回行って の起こる回数であったので、 回目の試行で、 が起こったとき(確率 )に 、 が起こらなかったとき(確率 )に という値をとる確率変数を考えて、それを とおくと、
と表されることになる。
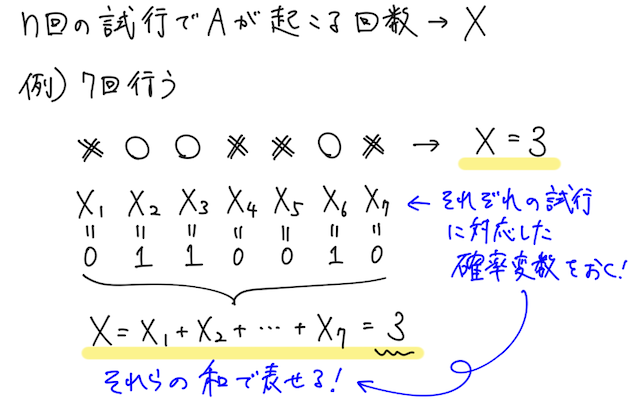
これを用いると、もっと簡単に の期待値と分散を求めることができる。
いま、和の期待値は期待値の和なので、 の期待値は
と表される。(ちなみに、この関係式は、確率変数同士が独立でなくても使える点を思い出しておこう)
ここで、確率変数 の期待値は、定義から
なので、 の期待値は
とすぐに求められる。
分散についても、それぞれの試行は独立なので、確率変数 、、...、 は独立である。よって、 の分散は分解できて、
と表される。
ここで、確率変数 の分散は、
であることを踏まえると、
と求められるので、 の分散は
とすぐに求められる。
正規分布による近似
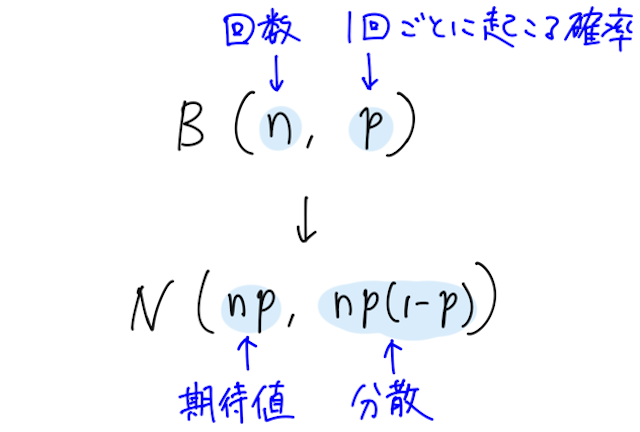
二項分布 に従う確率変数 は、 が十分に大きいとき、正規分布 に従うとみなせる(証明は大学でやる人はやる)。
これはとても重要な性質なので確実におさえておこう!!ややこしく見えるが、 が二項分布 に従うとき、期待値は 、分散は であるから、「分布の形が正規分布に近づくこと」だけ覚えておけばすぐに思い出せる。
二項分布と正規分布で、カッコの中に出てくるものが違うので、そこだけ区別しておこう。
また、正規分布に従うとみなせたら、標準化 を行い、確率変数 を
で定めれば、確率変数 は標準正規分布に従うとみなせることになり、標準正規分布表から確率などを計算していける。この流れは本当によく出てくるので、必ず頭に入れておこう!