## 概要

期待値の計算の基本を押さえよう。
**期待値の問題は定義が全て**なので、いつでも思い出せるようにしておくこと！

期待値を考えたい変量（下の例題でいうとゲームの得点）$X$ のとりうる値を $x_1, \ x_2, \ \cdots, \ x_n$ とし、$X$ がそれらの値をとる確率をそれぞれ $p_1, \ p_2, \ \cdots, \ p_n$ とするとき、$X$ の期待値 $E$ は

$$E=x_1p_1+x_2p_2+\cdots+x_np_n$$

で求めることができる。

つまり、**とりうる値をバーっと並べて、それらの確率をバーっと計算して、掛けて足していけばOK！**

## 例題

実際に解きながら確認しよう。

【問】サイコロを $1$ 回投げ、出た目の $3$ 倍を得点として与えるゲームを行う。このゲームの得点の期待値は何点か。

【答】今回は、得点の期待値を考えたいので、まずは**どんな得点があり得るか**を考えると、出る目

$$1, \ 2, \ 3, \ 4, \ 5, \ 6$$

の $3$ 倍なので

$$3, \ 6, \ 9, \ 12, \ 15, \ 18$$

の $6$ 種類である。

では次に、それぞれの得点をもらえる確率を考えると、全て $\dfrac{1}{6}$（さいころのそれぞれの出る目の確率に対応）なので、得点の期待値は、定義式より

$$
\begin{align}
&\small3\times\frac{1}{6}+6\times\frac{1}{6}+9\times\frac{1}{6}+12\times\frac{1}{6}+15\times\frac{1}{6}+18\times\frac{1}{6}\\\\
&=\frac{3+6+9+12+15+18}{6}\\\\
&=\frac{63}{6}\\\\
&=\frac{21}{2}
\end{align}
$$

と求められる。

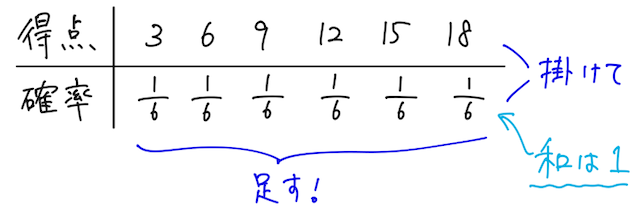
![Dr.okke3 P1.png](https://oke-files.s3.amazonaws.com/uploads/Z0bHLQaKbyl9V/a5b45bbfdafa409b8264778412e2f488.png)

※ 確率は、**足して $1$ になる**ことを確認するようにしよう！

### 補足

上の例のように、大体どれくらいの値が期待できるか、ということを表せるので **「期待値」** という名前も納得できる。

普段の生活でも、何か選ばないといけなくなったときに、自分が**それぞれの候補から得られるであろう期待値を計算する**ことで、意思決定をしやすくなることもある。

例えば、同じ値段の参考書を買うとして、

- 参考書 $A$ を買うと、$50$ %の確率で点数が $20$ 点上がり、$50$ %の確率で点数が $5$ 点上がる
- 参考書 $B$ を買うと、$20$ %の確率で点数が $40$ 点上がり、$80$ %の確率で点数は変わらない

という効果を見込めるとき、どっちを買うのが良いだろうか。

参考書 $A$ を買ったときの、点数アップの期待値は

$$20\times \frac{50}{100}+5\times \frac{50}{100}=12.5  \ \text{点}$$

参考書 $B$ を買ったときの、点数アップの期待値は

$$40\times \frac{20}{100}+0\times \frac{80}{100}=8  \ \text{点}$$

なので、参考書 $A$ を買おう、みたいな判断になる。

もちろん日常生活で、はっきりとそれぞれの結果になる確率を求められるケースは圧倒的に少ないが、**期待値で比較するクセ**を持っておくと論理的な人間に一歩近づけるのでおすすめ！

また、数学Ⅰのデータの分析や数学Bの統計分野で学ぶ **[「分散」](https://okke.app/words/p/hgvA3EHsJhven)** の考え方を組み合わせると、さらに良い判断ができる。

つまり、**期待値が同じであったとしても、結果の散らばり具合を表す分散が大きいと、リスクが高いので避けよう**、みたいな判断ができるようになる。（ここは人によって趣向が異なる。経済学の行動経済学という分野では、ここらへんの人間の心理を研究している）


期待値

概要

例題

補足

タグ