標本平均の分布

概要

母集団全体での平均を母平均、母集団全体での分散や標準偏差を母分散・母標準偏差という。

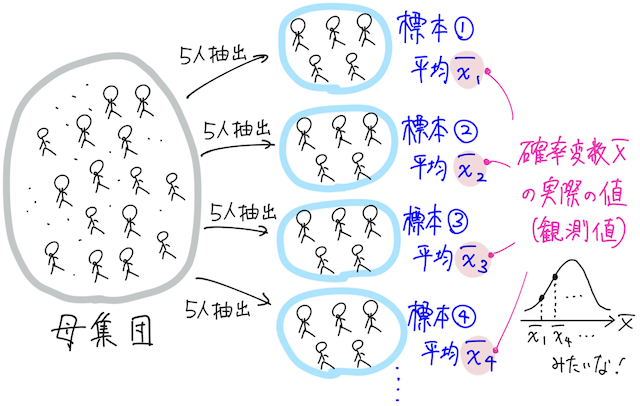
母集団から、無作為（ランダム）に大きさ の標本を抽出するとする。（「標本」はとりあえずデータのことだと思っておけばよく、要するに、母集団全体から 個のデータを選ぶということ）

このとき、抽出された標本 の平均

のことを標本平均と呼ぶ。

この標本平均 は、選ばれる標本によって変化するので、標本を何個も作ると、基本的には標本平均の実際の値はそれぞれ変わる。

クラスで 人ずつ集めて身長の平均を調べると、どの 人を集めるかで平均値って変わってくるよね、っていうこと。

つまり、標本平均は確率変数であり、標本平均の確率分布というものを考えられる。

確率変数としての標本平均 と、実際にとってきた標本の平均値（標本平均の観測値） の区別がとてもこんがらがりやすいので、注意しよう！

このとき、母集団の母平均を とし、母分散を とすると、標本平均 の期待値と分散は、母集団の値を用いて、

• （→ 母平均と同じ！）
• （→ 倍になる）

となる。この分散の値より、標準偏差は

と求められる。

分散や標準偏差が小さくなる件については、母集団から何個も取って、その標本の平均の値を考えているので、その平均の値のばらつきは、 個ずつのばらつきよりも確かに小さくなりそうだというイメージを持っておこう。

また、母集団がどのような分布になっていたとしても、独立な標本をたくさん取ってきて標本平均を考えれば、標本平均の確率分布は正規分布に近づくという性質がある（中心極限定理）。

つまり、標本が大きいと、標本分布は正規分布に従うとみなしてよいということで、これは本当にめちゃくちゃありがたい性質。もっと詳しくありがたみを感じたい人は、下の「補足②」のところを見てみよう。

期待値の証明

標本平均の期待値は母平均と一致するということを、数式でも押さえておこう。

母平均を とし、復元抽出する標本を とおくと、期待値の性質から

となる。（ちなみに、この期待値の和の分解は、別に確率変数同士が独立でなくても成り立つ点に注意）

いま、 はそれぞれ母集団全体から取り出しているため、それぞれの期待値は母平均である。つまり なので、

となって、確かに標本平均の期待値が母平均と一致することがわかる。

分散の証明

では、標本平均の分散が、母分散に比べてどのくらい小さくなるかを数式で確認しよう。これは結果もイメージもとても重要。

母分散を とし、復元抽出する標本を とおくと、これらの確率変数は独立なので、

である。（最後の変形は独立だから分解してOK！）

はそれぞれ母集団全体から取り出しているため、それぞれの分散は母分散である。つまり、 なので、

となって、確かに標本平均の分散は、母分散の 倍になることがわかる。

母集団から何個も取って、その平均の値を考えているので、 個ずつのばらつきよりは、ばらつきが小さくなるよねというイメージが大事！

補足①

ちなみに、非復元抽出（ 回抽出した標本を元に戻さない）の場合は、標本平均の期待値は復元抽出の場合と同じ、つまり母平均と一致するが、標本平均の分散は復元抽出の場合とズレることになる。

※ 詳しくは省略するが、母集団の大きさを とすると、非復元抽出での標本平均の分布は、 になってしまう。上の導出で、分散の和の分解が綺麗にできなくなる。

しかし、標本の大きさに比べて母集団が大きくなると、重複して取り出す可能性が小さくなるので、そのズレは無視できるものになっていき、非復元抽出であっても復元抽出とほぼ同じものを見なすことができるので、上の公式を用いてOK。

※ 確かに上の式でも、 に比べて、母集団の大きさ が十分大きくなると

となって、復元抽出の場合と同じとみなせる。

補足②

なぜこんな「標本平均」というものをわざわざ考えるのだろうか？

これは、母集団がどのようなものかわからないときに威力を発揮する。

詳しくは「母平均の推定」という用語ページ（全力で作成中）で解説するが、例えば母集団全体の分布や母平均がわからないとする。

そういう状況であっても、たくさんの標本をとってきて、標本平均などの値を求めることはできる。

標本が十分大きいと、元の分布の形がわからなくても、標本平均の分布は正規分布とみなせるので、標本平均の実際の観測値や、その正規分布の形を使って、だいたい母平均がどのくらいか推定することができるのである。

これが標本平均を考えることの醍醐味の一つで、母集団の状況がはっきりわかることの方が少ない実社会でも数多く応用されている。例えば、日本中の人に 人ずつ聞いて統計を取っていくことはあまり現実的ではないが、ある程度多くの標本をとって、標本平均というものを考えることで、日本全体についての大まかな様子がわかるというのがすごいところ！