対偶
概要
(※ 命題という言葉が
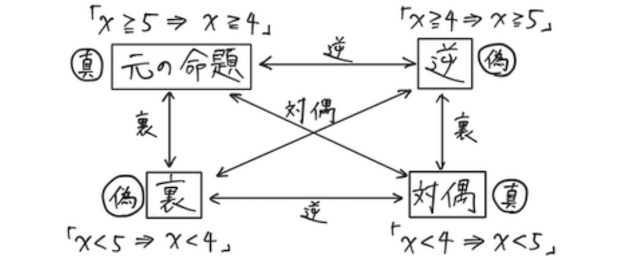
命題「
命題の対偶は、 元の命題と真偽(つまり正しいかどうか)が必ず一致する(逆や裏には無い、ありがたポイント)。つまり、命題が真なら、その対偶も真。命題が偽なら、その対偶も偽。
なので、元の命題の真偽(つまり正しいかどうか)がわかりにくい時に、対偶の命題の真偽を示すことで、元の命題の真偽が示せる。
例
【問題】整数
【解答】示したい命題の対偶を取ると、「
また、対偶は、命題の逆の裏、命題の裏の逆と考えることもできる。
この用語を含むファイル
関連動画
(※ 命題という言葉が
命題「
命題の対偶は、 元の命題と真偽(つまり正しいかどうか)が必ず一致する(逆や裏には無い、ありがたポイント)。つまり、命題が真なら、その対偶も真。命題が偽なら、その対偶も偽。
なので、元の命題の真偽(つまり正しいかどうか)がわかりにくい時に、対偶の命題の真偽を示すことで、元の命題の真偽が示せる。
【問題】整数
【解答】示したい命題の対偶を取ると、「
また、対偶は、命題の逆の裏、命題の裏の逆と考えることもできる。

この用語を含むファイル
関連動画