運動エネルギー

概要

質量 の物体が速さ で運動しているとき、 をその物体が持つ運動エネルギーと呼ぶ。

つまり、質量があって動いている物体は、運動エネルギーを持っていて、エネルギーを持っていると仕事をする能力を持つことになる。

また、上で「速さ」を用いて定義したように、この運動エネルギーは向きの情報をもなたい。かっこよく言うと、スカラー量である。なので、平面や空間で物体が動いていても、運動エネルギーは成分に分けることができないし、また負の値も取らないことに注意しよう。

ちなみに、平面や空間での運動について、速さ の 乗は、速度の成分 を用いて次のようにして求められる。

仕事との関係

実は、ある時刻からある時刻までの物体の運動エネルギーの変化は、その間に物体が受けた仕事に等しい。これはとても重要な関係。（仕事の辞書はこちらから）

まずは簡単なケースで考えてみよう。いま、なめらかな水平面上で、質量 の物体が一定の力 を受けて直線的に運動していて、ある時間に距離 だけ進み、速度は から に変化したとする。

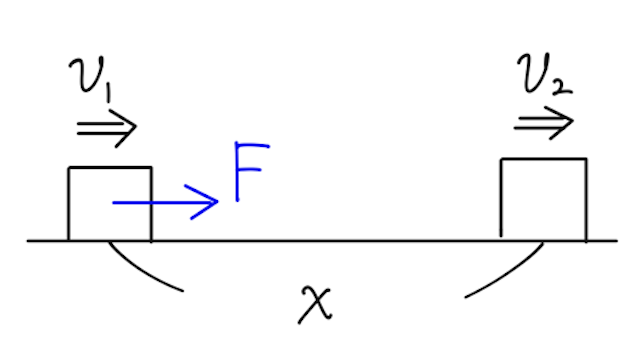
このとき物体の加速度を とおくと、運動方程式より

等加速度直線運動の式より

となる。このとき、運動エネルギーの変化は、

となって、確かに物体が受けた仕事（＝力 が物体にした仕事）に等しいことがわかる。

また、この関係式から、運動エネルギーの単位はジュール とも表されることがわかるので、運動エネルギーの定義から出てくる の次元と、 の次元が等しいことがわかる。（出した解答の変数漏れや指数間違いのチェックなどにとてもよく使える！）

発展

上で証明っぽいものを考えたが、実際にはこの仕事との関係式は、力が一定じゃなくても成り立つ関係。これを微積の知識を使って示しておく。ここでは直線上の運動を引き続き考えるが、平面や空間になっても成分に切り分けて積分していくだけなので、やることは同じ。

なお、動画で学びたい！ という方には、東大物理学科卒ひぐまさんの動画がオススメ。仕事と運動エネルギーの関係について、数学的に深く学べる。

始まりの時刻を 、位置を 、終わりの時刻を 、位置を とおく。

運動方程式より、

ここで、両辺に をかけて、両辺を で から まで定積分する。

※ の積分から や の積分に変わっていて、それぞれの変数に対応する積分区間に変わっていることに注意。（置換積分の辞書）

①の左辺を計算すると、

となり、運動エネルギーの変化を表す。

また、①の右辺は、力 が物体にした仕事、つまり物体が力 から受けた仕事を表す（仕事の辞書を参照）ので、運動エネルギーの変化は、物体が受けた仕事に等しいことがわかる。