力積と運動量の関係

概要

質量 の物体が時間 の間に力積 を受けて、速度が から に変化したとき、物体の運動量と物体が受けた力積の間に、次の関係式が成り立つ。

また、力 が時間によらず一定の場合は、力積は

と表されるので、力積と運動量の関係は

と表すことができる。

運動量と力積はベクトルであることに注意が必要で、この関係式もベクトルの式になっている。つまり、成分に分けて式を立てることができる。例えば平面上で運動していて、速度や受けた力積の 成分が 、、、 成分が 、、 だとすると、

と各成分で関係式が成立する。実際に使う場合は、このように成分ごとに考えるのがほとんど。

この関係式の使い方としては、

• や がわかっているもしくは計算できるときに、 を求める。
• と がわかっていて、運動量変化から力積 を求める。

ことが多い。

導出

使えればいいじゃないか！という声もある一方で、導出まで納得しておくと思い出しやすいし、物理の応用力につながるので、是非考えてみよう。

まずは基礎編として、力が時間によらず一定の場合を考える。力 が時間 の間に物体に作用し、物体の速度が から に変化したとする。このとき、運動方程式より

※力が一定なので、加速度は時間 の間一定であり、 で求められることに注意。

両辺に をかければ、

となり、運動量変化＝力積の関係式が示される。

では発展編として、力が一定ではない場合を考える。（「俺は物理の強者になりたいんじゃ〜！」という方向けなので、興味なければ読み飛ばしてください）よくわからない！ という方は、東大物理学科卒ひぐまさんの動画がオススメ。

ベクトルのまま計算すると、積分などがややこしく見えるので、まず 成分で議論していく（ここでは平面上の運動を考えるが、空間でも同様）。また時間 は、時刻 から までとし、物体にはたらく力は

とおく（各成分は の関数であることに注意）。このとき、力積は定義より

となる。また、運動方程式より

と変形できる。（詳しくは、運動量の辞書を参照）これを時刻 から まで時間で積分して変形していくと、

となって示される。

※ 左辺は、 の積分から の積分に変わっていて、対応する積分区間に変わっていることに注意。（置換積分の辞書）

成分についても同様にして、

が示されるので、ベクトルの形にまとめて

が成り立つ。

補足

この、運動量変化は物体が受けた力積に等しい、というのと似た関係に、運動エネルギーの変化は物体がされた仕事に等しい、という関係がある（運動エネルギーの辞書で確認しよう）。

物理の美しさが詰まったテーマである一方で、とてもよくこんがらがるので、ここで整理しておこう。

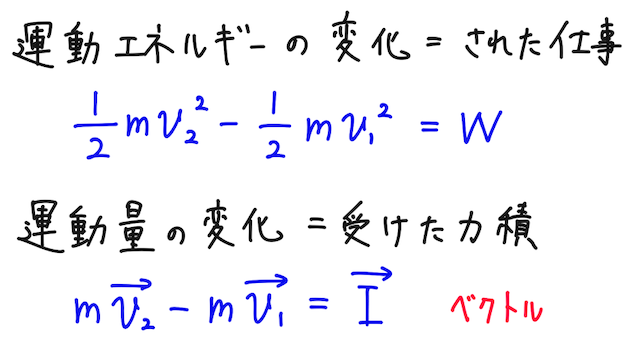
• 運動エネルギーの変化＝された仕事、の関係式は、スカラーの関係式であり、成分という概念がない。（力には成分があるんだけどね）
• 運動量の変化＝受けた力積、の関係式は、ベクトルの関係式であり、成分に分けて考えることができる。