仕事率

概要

仕事を考えるときには（ここは物理の世界の「仕事」を考えることにしよう！）、仕事の「量」だけを考えてきた。じゃあその仕事がどれくらいの時間で行われたのか、言い方を変えると、どれくらい効率よく仕事を行ったのか、について考えたいことがある。

そのときに出てくるのが仕事率という概念だ。時間 の間に力がする仕事が のとき、

を、この時間内での （平均の）仕事率という。仕事量を時間で割るだけ。単位はワット で、上の式から の次元は に等しい。

仕事量としての と、仕事率の単位としての がぐちゃぐちゃになりやすいので、気をつけよう。

仕事率は現実世界でもイメージすることができて、仕事率は 「仕事の効率」 くらいに思っておけばOK。ここでは宿題をすることを「仕事」だと思うことにすると、例えば同じ量の宿題をAさんは30分で終わらせたものの、Bくんは3時間かかったとする。このとき、Aさんは仕事の効率が大きい、つまり仕事率が大きい、と言える。

例

【問】あらい水平面上に質量 の物体を乗せ、外力 で物体を引っ張り、一定の速さ で時間 だけ移動させた。このとき、外力 のした仕事と仕事率を を用いずに求めよ。ただし、動摩擦係数を とする。

【答】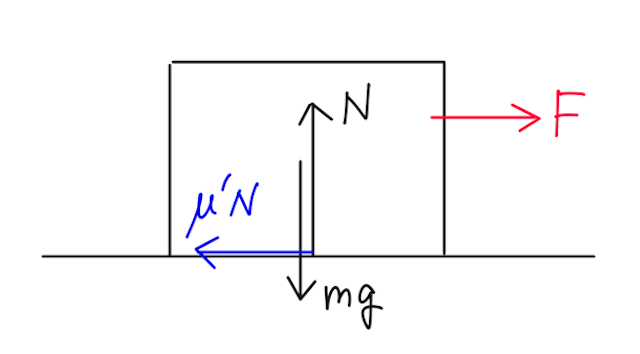

鉛直方向の力のつり合いより、

加速度 より、水平方向も力はつり合っており、

これらより、

と求められる。移動による変位は なので、求める仕事 は、

となる。また、仕事率 は

となる。

補足

上では、仕事量の時間に対する割合が常に一定である場合を扱ったものの、現実はそんなに甘くない。仕事量の時間に対する割合が時間によって変わる場合は、時間を細かくしていって、微小時間 における仕事量 の割合を瞬間の仕事率として考える。（考え方としては、平均の速度・瞬間の速度と同じ！）

仕事の式（）を用いると、このような表し方ができる。（ここでは、力や、力と変位の向きは時間によらず一定とする）

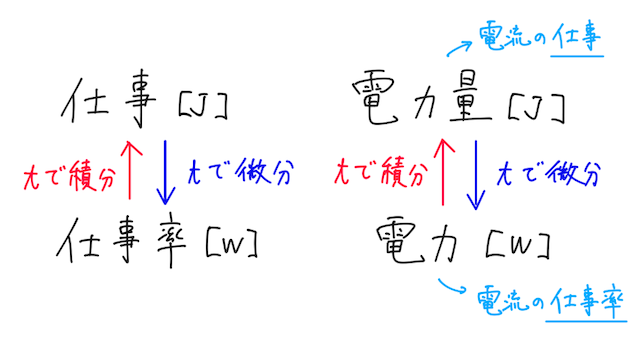
微分を学んでいる方は、仕事の時間微分が仕事率である とスッキリ理解しよう。変位の時間微分が速度になるのと、同じイメージ。

また、電磁気まで学習した人は、 「電力」「電力量」 という用語を知っているかもしれない。電力は、単位時間に電流がする仕事、つまり電流がする仕事率 と考えることができ、電力量は、電力を時間積分した電流の仕事 なので、注意しよう。（とてもよくこんがらがる！）