気体分子運動論

はじめに

気体の圧力や体積といった、気体分子がめちゃくちゃたくさん集まったものについての情報を、1個1個の気体分子についての質量や速度といった情報で表せないか考えてみよう。

気体全体の圧力や体積（）を、1個1個の気体分子についての質量や速度（）で表しつつ、結論としては、この単原子分子の内部エネルギーの式

を示すのがゴール。

結構長い話になるけども、今から紹介していくストーリーは教科書にも載っていて、よく 「気体分子運動論」 と呼ばれ、このまままるっと入試に出ることも多いので、自力で最初から最後まで再現できるように身につけておこう。

状況の設定

一辺の長さが 、体積 の立方体の容器を用意して、そこに1個の質量が の単原子分子を 個入れた状況を考える。

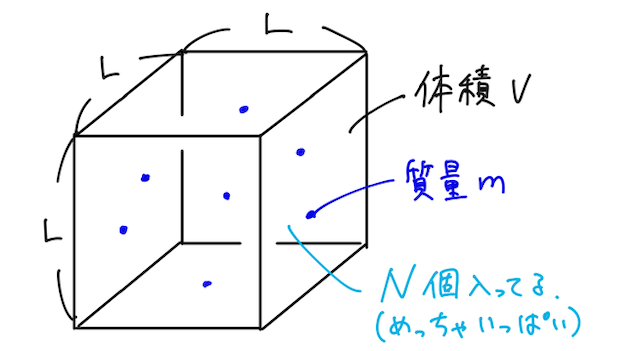
現実の気体をいきなり考えられるほど世の中甘くないので、議論できるように理想的な設定を仮定していく。

仮定①：分子は立方体の容器内をビュンビュン飛び回り、立方体の壁に衝突しまくるが、その衝突は 弾性衝突 であるとする。

仮定②： 分子の数（）はめちゃくちゃ大きく、分子は平均的に見たときに特定の方向に偏って運動しておらず、どの方向の平均の速度も等しいとする。（分子運動の等方性という）

仮定③： 分子間にはたらく力を無視できる理想気体としての単原子分子を考える。このとき、気体の内部エネルギーは、それぞれの気体分子の運動エネルギーの合計と考えてよい。

これらを認めた上で、導出を見ていこう！

内部エネルギーの式の導出

まず、気体全体の圧力や体積（）を、1個1個の気体分子についての質量や速度（）で表すことをやっていこう。

1個1個の分子の衝突について、じっくり考えてみる。

立方体の辺に沿って例えば左下のように 軸、 軸、 軸を設定する。

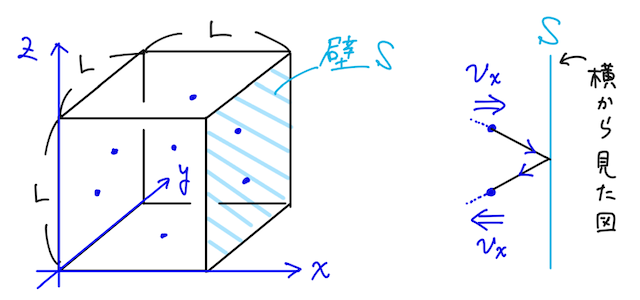
まずは 軸方向の運動に注目して、ある壁 に衝突する直前の 軸方向の速度を とおく。

このとき、仮定①より衝突後の速度は となるので、衝突により気体分子が受ける力積は、運動量と力積の関係より

となる。作用反作用の法則から、1個の分子の衝突により、気体分子から壁が受ける力積の大きさは、

と求められる。

また、一度壁に衝突した気体分子が、向かいの壁でも衝突し、再び同じ壁 に衝突するまでの時間は、 軸方向の移動距離 を 軸方向の速さ で割って、

と求められるので、まとめると、壁 は1つの気体分子から、 ごとに大きさ の力積を受けることになる。

よって、時間 の間に、壁 が1つの気体分子から受ける力積は

となる。

この間に、壁 が1つの気体分子から受ける平均の力の大きさを とおくと、上の力積を時間 で割って

と求められる。

これはあくまでも1個の気体分子から受ける平均の力の大きさであり、壁 が 個の気体分子から受ける平均の力の大きさ は、気体分子全体での の平均値を とおけば、

と表される。

ここで、他の軸の方向の速度も考えてみると、まず分子の速度 について一般に

であるから（下の図で、三平方の定理で考えてみよう）

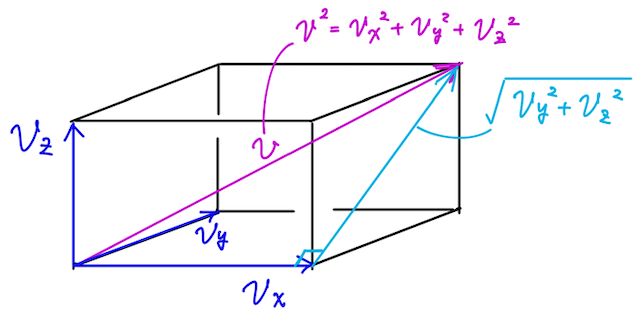
が成り立ち、さらに今回は仮定②の分子運動の等方性より

としてよいので、

が成り立つ。

よって、これを 式に代入すれば

と整理できる。

ここまでくれば、平均の力の大きさ を壁 の面積（）で割ることで気体全体の圧力 を求めることができ、

となるので、

が成り立つ。

つまりこれで、気体全体の圧力や体積（）を、1個1個の気体分子についての質量や速度（）で表すことができたことになる！

ここで、気体の温度を 、物質量を とすると、理想気体の状態方程式より、

なので、 式に代入すると

を得る。左辺が気体分子1個の運動エネルギーの形になるように変形すると

となる。ここでアボガドロ定数を とすると、定義から

なので、 式は

と表せる。ここで、 は気体定数をアボガドロ定数で割ったただの定数であるから、これをまとめて という定数で表すと、

が導かれる。

この、気体定数をアボガドロ定数で割った定数 をボルツマン定数と呼ぶ。値としては

となる。

式はとても重要で、これは、理想気体では、気体分子の平均の運動エネルギーが温度だけで決まり、絶対温度に比例することを表している。

さらに、単原子分子理想気体の内部エネルギーは、仮定③により、気体分子の運動エネルギーの総和で求められるので、 式より

となり、確かに単原子分子の内部エネルギーの式が示された。

補足

余裕がある人は、気体の二乗平均速度という物理量についても求め方を学んでおこう。