奇関数の積分

概要

が成り立つとき、 を奇関数といい、グラフは原点に関して対称となる。この奇関数の積分は、ラクをすることができて、

が成り立つ。積分区間が 逆 になっていることが大事。グラフのイメージでも理解しておこう。

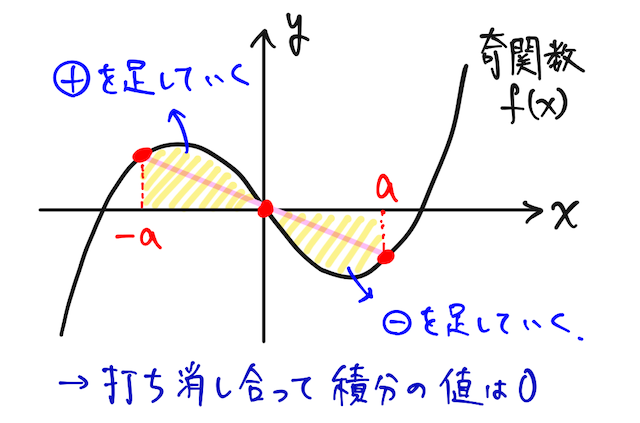
積分区間を を境に分けて、上の奇関数の性質と、数学IIIで学ぶ置換積分を使うと、厳密に証明もできるので、興味のある人はやってみよう。

例

【問１】（数学III）

の値を求めよ。

【答】真面目に部分積分しても解けるが、積分の中身の関数が奇関数であることに気付くと一瞬で とわかる。実際に、

とおくと、

となるので、

が成り立つので、 は奇関数。よって、 から まで積分すると になる。

このことから、 は偶関数だが、奇関数である をかけた は奇関数になることがわかる。

【問２】

の値を求めよ。

【答】真面目に全ての項を積分しても解けるが、積分の中身の項が、ところどころ奇関数になっていることに気付くと、少しラクができる。さらに、残りの関数も偶関数になっていることに気づけば、さらに幸せ。つまり、

や は奇関数（気になる人は に を代入してみよう）なので、

が成り立ち、さらに、残りの項の や は 偶関数なので、その積分の性質から、

となることを利用すると、

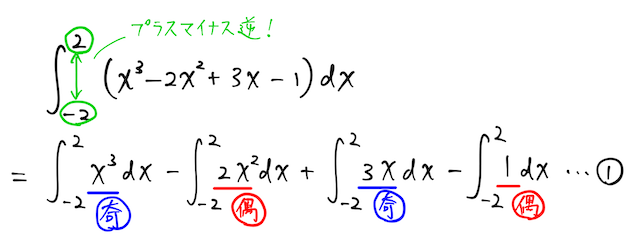
と計算できる（ここでは丁寧に変形していったが、慣れていくと、 行目から 行目にジャンプするくらいの勢いになる）。

計算量が減るし、ミスも減る！

補足

多項式や、三角関数がからむ積分では、このワザを頭に入れておくとお得な場面が多々ある。特に、奇数乗しか登場しない多項式は奇関数だと見抜けるようになろう。

係数が奇数・偶数かどうかとは、全く関係がない概念なので、要注意。