偶関数

概要

が成り立つとき、 を偶関数といい、グラフは 軸に関して対称となる。偶関数かどうかを確かめるには、 の に を代入してみて、 もとの と一致するか を確かめればOK。

例

【例１】

は偶関数である。

なぜなら、 の に を代入 すると、

となり、

が成り立つため。（最後の の変形がわからなかった方は、この180°関係の辞書を復習しよう！）

グラフからも明らか。

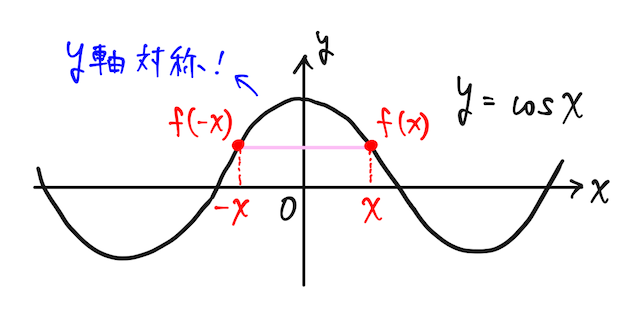
実はこのテーマは三角関数の話にとどまらず、一般的に言える。例えば、

【例２】

は偶関数である。

なぜなら、 の に を代入 すると、

となり、

が成り立つため。

グラフは下のようになり、グラフからも明らか。

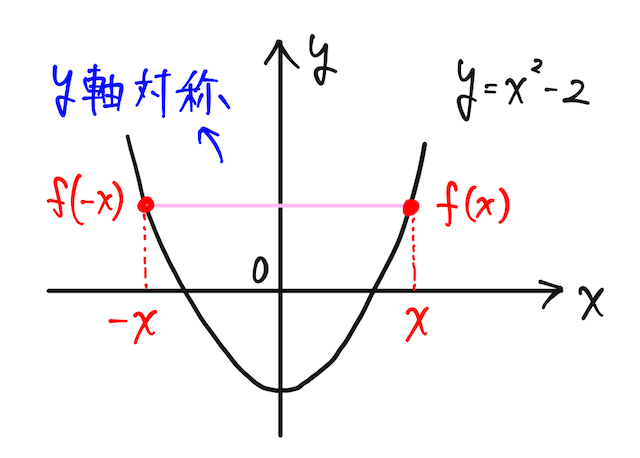
補足

なんでこんなものを考えるかというと、偶関数であることに気付くと積分計算が楽になることがあるため。実は、 が偶関数のとき、

が成り立ち、積分区間の片っぽが になり、代入計算がラクになって幸せ。詳しくは、この偶関数の積分の辞書で確認しよう。

また、兄弟分の奇関数 については、こちらの奇関数の辞書から確認しよう！