偶関数の積分

概要

が成り立つとき、 を偶関数といい、グラフは 軸に関して対称となる。この偶関数の積分は、少しラクをすることができて、

が成り立つ。積分区間が 逆 になっていることが大事。さらに、定積分の代入計算で を代入すればいいというのが、とてもありがたい。

グラフのイメージでも理解しておこう。

積分区間を を境に分けて、上の偶関数の性質と、数学IIIで学ぶ置換積分を使うと、厳密に証明もできるので、興味のある人はやってみよう。

例

【問】

の値を求めよ。

【答】真面目に全ての項を積分しても解けるが、積分の中身の項が、ところどころ奇関数や偶関数になっていることに気付くと、幸せになれる。つまり、

や は奇関数（気になる人は に を代入してみよう）なので、その積分の性質から、

が成り立ち、さらに、残りの項の や は偶関数なので、

となることを利用すると、

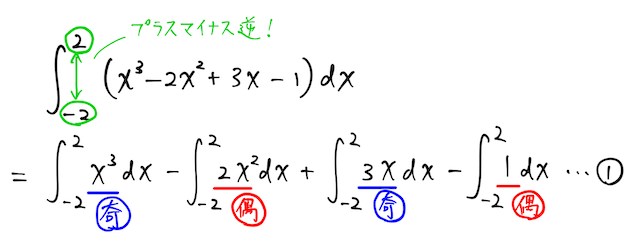
と計算できる（ここでは丁寧に変形していったが、慣れていくと、 行目から 行目にジャンプするくらいの勢いになる）。

計算量が減るし、ミスも減る！

補足

そもそも積分を計算しなくていい奇関数の積分ほどのインパクトはないが、多項式の積分では役に立つことが多い。特に、偶数乗しか登場しない多項式は偶関数だと見抜けるようになろう。

係数が奇数・偶数かどうかとは、全く関係がない概念なので、要注意。