エネルギー準位

ラザフォードの原子模型をもとに、デンマークの物理学者であるボーアはいくつかの仮説を設定し、水素原子のスペクトルのとびとびの波長を求める式を導くことに成功した。（詳しいストーリーは、ボーア半径の解説を参照）

この用語では、そんな水素原子のスペクトルの式の導出を解説していく。（全体を通して、文字が多くてやる気が原子核くらいちっちゃくなるかもしれないが、大した計算はしてないので、頭の中ででも紙に書きながらでも頑張って追っていこう）

エネルギー準位の計算

ボーアは量子条件という仮説をおき、電子のエネルギーはとびとびの値（エネルギー準位）をとるとされたのであった。そこでまずはボーアの仮定したエネルギー準位の式について考えてみよう。

ボーア半径の式を導いたときと同様に、水素原子において、電気量 の原子核の周りを、質量が 、速さが 、軌道の半径が で等速円運動する電子を考える。

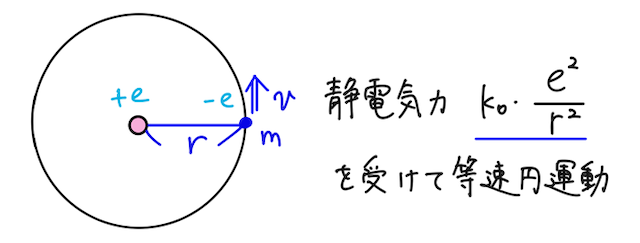
この電子のエネルギー は、無限遠を基準にとると、

• 運動エネルギー：
• 静電気力による位置エネルギー：（原子核が作る電位の式に、電子の電気量（）をかける）

の合計であるから、

と表せる。（いまのところ は現れてないが、後で に対応した値になることがわかるので、 とおいている）

ここで、等速円運動の運動方程式より

なので、 式に代入して、

を得る。ここで、ボーア半径の式 より

なので、これを 式に代入して、

となって、水素原子のエネルギー準位の式が求められた！

ここで、 のとき、つまり軌道半径が一番小さくエネルギーも一番低い状態を基底状態といい、 と軌道半径が大きくなりエネルギーが大きくなった状態を励起状態というので、頭の片隅においておこう。

水素原子のスペクトルの式の導出

ではこの、水素原子のスペクトルのとびとびの波長を求める式を導出していこう。

ボーアの振動数条件 から、定常状態 から別の定常状態 （ とする）に移るとき、1個の光子のエネルギーが放出され、

となるのであった。

ここで、この放出された光の波長を とおくと、光の速さと振動数との間には

が成り立つ（これはただの波の基本式）ので、 式を使って を消去すると

となる。ここで 式のエネルギー準位の式を用いると、

を得る。ここで定数部分をまとめて

（リュードベリ定数）とおくと

が導かれる。このようにして、ボーアは、水素原子のスペクトルを理論的に説明することに成功したのである。