波の基本式
概要
波を伝えるものを媒質といい、ある時刻での媒質の変位(どれくらい動いているか)を示す曲線を波形という。
よく間違いそうになるのが、波が伝わるときは、媒質がそのまま吹っ飛んでいっているのではなくて、媒質の各部分はわずかに振動するだけであり、その振動が伝わって波になっている。例えば、音の媒質は空気であるが、音源の近くの空気が、物理的にそのまま耳まで吹っ飛んできているわけではない。
ここでは、波を表す要素(用語と定義)をいくつか押さえて、波の分野でむちゃんこ大事な、この波の基本式を押さえよう。
この式は、波動を勉強するとわんさか出てくるが、日本語の定義から納得しておけば、忘れないのでオススメ。
波の要素の定義
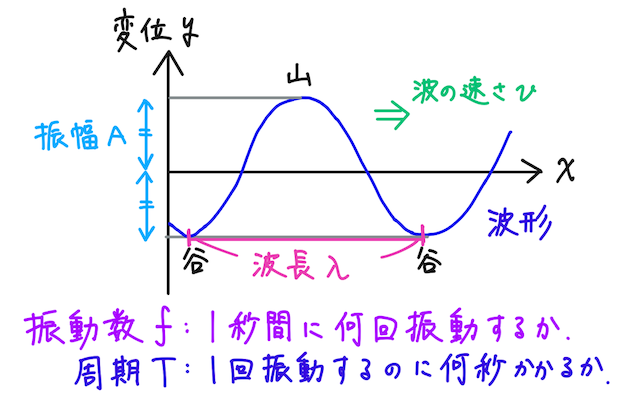
-
まず、波形は、媒質により決まる速さで移動していき、その速さを波の速さといい、
で表す。単位は 。「え、媒質がそのまま物理的に動いていくわけじゃないのに、なんで速さがわかるの?」という疑問を持つかもしれない。ここで定義された 「波の速さ」というのは、振動する媒質の各部分そのものの動きの速さではなくて、媒質が伝わっていくその伝播の速さとして定義されているので、注意しよう。 -
隣り合う山と山、谷と谷のように、振動の状態が同じ隣り合う
点間の距離を波長といい、 で表す。単位は 。また、振動の状態が同じことを位相が等しいという。( がうまく書けないときは、漢字の「入」を書いておけばとりあえずごまかせる) -
媒質中の
点の変位の大きさの最大値を、その波の振幅といい、よく で表す。波形の一番高いところである山の変位、と考えることもできる。単位は 。 -
媒質中の
点が、 秒間に振動する回数を、その波の振動数という。山から山など、同じ状態に戻ってきたら 回の振動とカウントする。元の位置に戻ったら 回とカウントされるシャトルランとは、数え方が違うので要注意。振動数は で表し、単位はヘルツ と呼ばれる。振動数が大きいほど高音になる。 -
媒質中の
点の振動の周期、つまり次に同じ状態に戻ってくるまでの時間を、その波の周期といい、 で表す。例えば、波の山であった位置が再び波の山になるまでの時間、ということもできる。
波の基本式
上の各定義は必ず頭に入れた上で、まず大事な関係式がコレ。
これは例えば、
さらに、波の速さは、
が成り立つ。単位で考えても、両辺
ここに、上の振動数と周期の関係を用いると、
が導かれる。これをよく波の基本式と呼び、波の分野ではこれを知っていないと話が始まらないと言ってもいいくらいの大事な式なので、頭に入れておこう。
例
【問1】振動数
【答1】波の基本式より、
言葉で理解すると、
【問2】図のように、
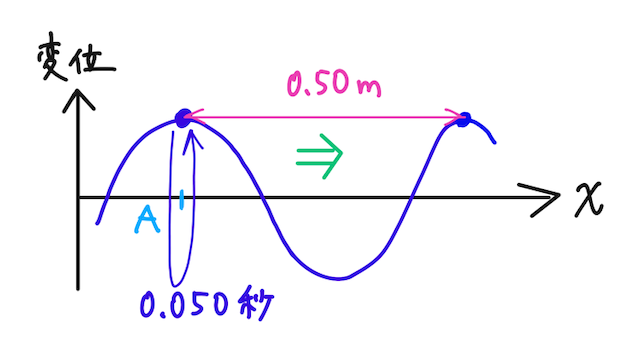
【答2】波の基本式より、
言葉で理解すると、波が
補足
動画でイメージをつかみたい!という方は、みっきーさんの動画や、Try ITの鈴木先生の動画(ひもが登場する)を確認しよう!
関連動画
関連用語





