等速円運動

概要

物体が円周上を一定の速さで回るような運動を、等速円運動という。メリーゴーランドのイメージ（速度が変わるようなゴージャス版は考えない）。

等速円運動では、動く方向が刻一刻と変わっていき、これまでの運動のように 軸や 軸で分解して運動方程式を考えてもうまく処理ができないので、特別な場合として運動を考える必要がある。

結論としては、等速円運動の速さを 、角速度を 、半径を とすると、

• 等速円運動の速度：接線方向に
• 等速円運動の加速度：中心方向に （中心向きの向心力により生じる）

となる。

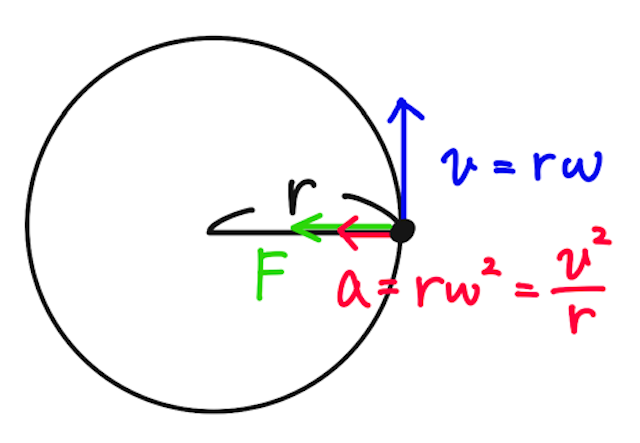
特に加速度は導出が少し大変なので、解いていくうちに覚えてしまうのが理想的。とはいえ、一度は順を追って導出してみよう。

等速円運動の速度

まず、角速度という新しい物理量を温かく受け入れてあげよう。

円運動をする物体の単位時間あたりの回転角を角速度といい、 で表す。時間で割っているし、角度についての速度っぽいので、この名前になっている。角の測り方は弧度法を用いるので、角速度の単位は となる。

これを使って、等速円運動の速度について考えよう。半径 の等速円運動で、時間 の間に角度 だけ回転したとすると、弧度法の定義から、物体が移動した距離 は、

である。よって、等速円運動する物体の速さ は、

と求められる。この式は、とてもよく使うので、いつでも取り出せるようにしておこう。

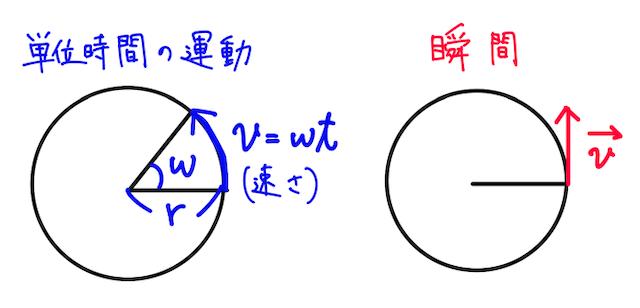
イメージとしては、 は弧度法で測った単位時間あたりの回転角なので、半径に をかければ、単位時間あたりの円周上の移動距離が出る（つまり速さ）、という感覚を持っておけばいつでも思い出せる。

「速度」を考える上で、もう一つ決めないといけないのが向きであるが、等速円運動の速度の向きは、円の接線方向となる。これはイメージでも理解できる。

よってまとめると、等速円運動の速度は、

• 向き：接線方向
• 大きさ：

となる。

※ 上の計算から、「あれ？速度の向きは、円周に沿ったような向きになるのでは？」と感じる方もいるかもしれないが、ここでは 「瞬間の速度」 を考えているので、限りなく短い時間を考えていくと、その時点での接線の向きに速度が生じていることが分かる。（速度の大きさである速さについては、ここでは等速円運動を考えているので、上のように長めの時間を取って考えても値は変わらない）

等速円運動の加速度

では次に、加速度を見ていこう。等速円運動では、速さが一定なので、「加速度ないんじゃね？」というポジティブ星人が多く発生する。

しかしながら、上で見たように速度の向きが刻一刻と変化していくため、速度自体は変化している。 よって加速度も生じることになる。定義からしっかりと考えてみよう。

まず、上と同様に、半径 の円周上を角速度 で等速円運動する物体を考える。このとき、短い時間 の間に物体が角 だけ回転し、速度ベクトルが から に変化したとする。

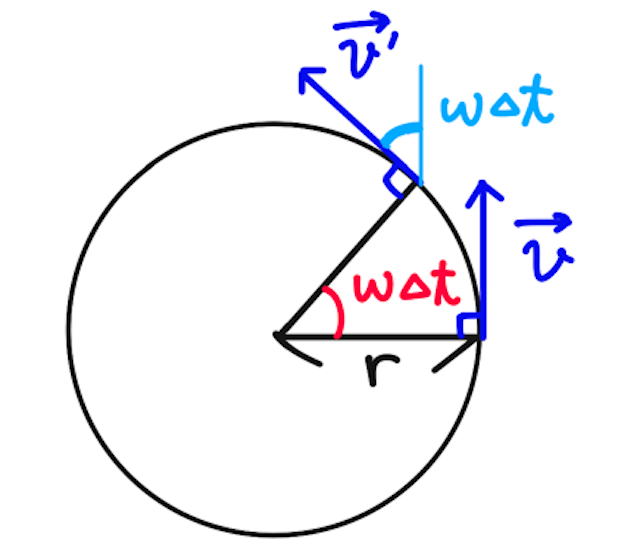
等速円運動を考えており、ベクトル と の大きさ（つまり速さ、これを とおく）は等しく、なす角は となる。

速度の変化ベクトル を考える。これもベクトルであることに注意。図示すると、下のようなベクトル（）を表している。

ここで、求めたい加速度ベクトル は、速度の変化ベクトルを時間で割って、限りなく時間を短くしていったものである。よって、 を十分短い時間として、

を考えれば良い。

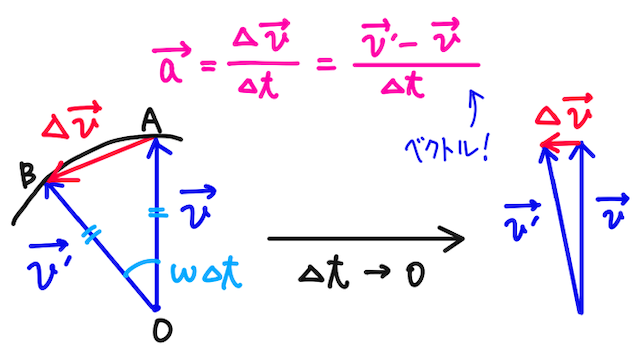
時間 を限りなく短くしていくと、図のように、速度の変化ベクトル は、速度ベクトル に垂直な向きになっていく。よって、それを という値で割っている加速度ベクトル も、速度ベクトル に垂直な向き、つまり円の中心方向を向くことがわかる。

では、加速度ベクトル の大きさ を求めよう。

ここで、十分に時間 が短いとき、

となるので、

を得る。 であることを用いると

と変形できる。これは等速円運動でとても大事な式で、この2つの形はどっちもよく使うので押さえておこう。

よってまとめると、等速円運動の加速度は、

• 向き：中心方向
• 大きさ： もしくは

となる。

等速円運動の運動方程式

等速円運動の加速度が、中心方向を向いていて、値が一定ということは、運動方程式より、物体は中心向きに何かしらの一定の力を受けていることがわかる。その力のことを向心力という。

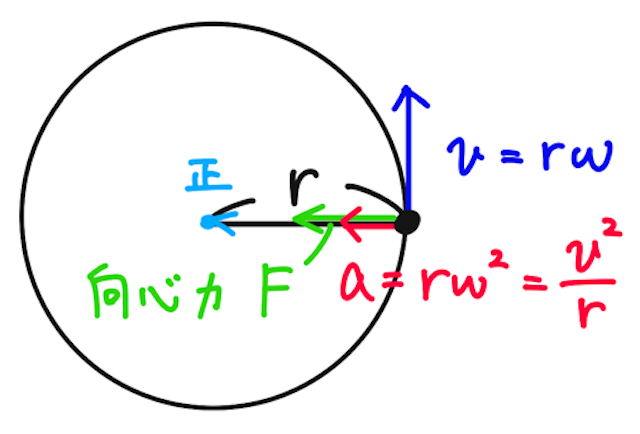
向心力の大きさを とすると、等速円運動の中心方向の運動方程式は、

もしくは

で表される。等速円運動ではこの式を立てられなければジ・エンドな問題も多いので、必ず頭に入れておこう。また、等速でないような円運動（例えばジェットコースターみたいなの）でも、半径がもし一定であれば、中心方向の運動方程式は上記の式で考えられる。（この場合は、 の方の式を使うことが圧倒的に多い）

（発展）微積で理解

では、上の等速円運動の速度・加速度を、微分の知識を用いて綺麗に示してみよう。

座標平面上で、原点 の周りを、半径 の円周上を角速度 で等速円運動する物体 を考える。

が 軸の正の側を横切るときを時刻 とすると、各時刻 での の位置は、円の媒介変数表示を用いて、

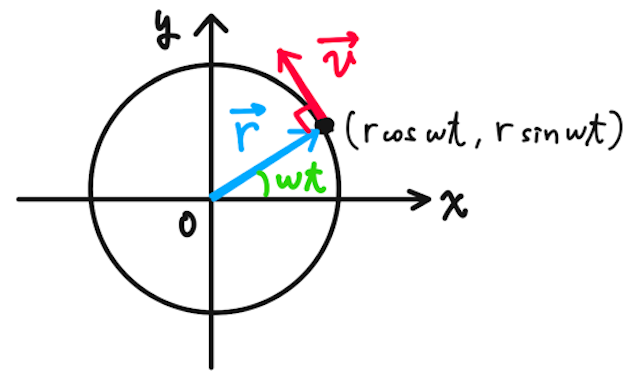
と表される。速度ベクトルは、位置ベクトルを成分ごとに時間で微分することで求めることができ、

となる（三角関数の導関数の辞書はこちらから）。ここで、位置ベクトル との内積を成分計算すると、

が分かるので、速度は接線方向であることがわかる。

では、速度の大きさである速さは、

と確かに上で求めた結果と一致する。（三角比の公式を用いた）

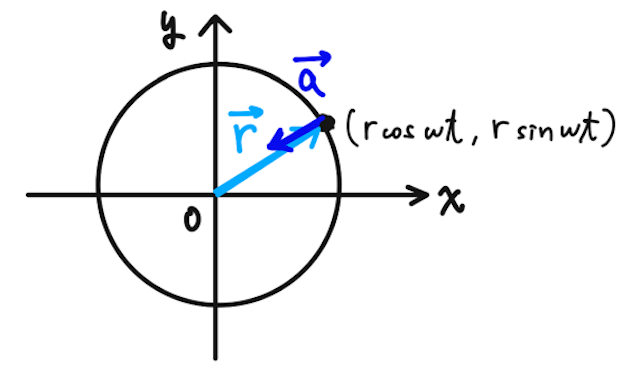
では、加速度ベクトル を求めよう。加速度ベクトルは、速度ベクトルを成分ごとに時間で微分することで求めることができ、

となる（三角関数の導関数の辞書はこちらから）。この結果から、位置ベクトルと平行で、逆の向きになることがわかる。つまり中心方向を向く。

では、加速度の大きさを求めると、

と確かに上で求めた結果と一致することが分かる。（三角比の公式を用いた）

補足

では等速でないような円運動や、半径が一定でない場合はどのように考えるのか？という疑問が出てくるが、これについての運動方程式を考えていくのは割と発展的になるので、別の辞書で見ていくことにする。こちらの 極座標系の運動方程式の辞書 を参照。

そちらの辞書でも触れている通り、等速でないような円運動でも、中心方向の運動方程式は上記の式で考えられる。

運動方程式が複雑になるので、そのような場合は つの時点間で議論ができるエネルギー保存則などを用いて解いていくことになる。