ボーア半径

原子の構造をめぐる歴史

原子は、正電荷が集中しためっちゃ小さい原子核と、その周りをビュンビュン回る電子からなるというモデルは、いまでは教科書に載っているくらい当たり前のことだが、実はこれは今からさかのぼることたった100年くらい前の、20世紀初めに発見された。

正に帯電した球の中を電子が回っていると考えたトムソンの原子模型や、正の電気量をもった球の外側を電子が回っていると考えた長岡半太郎の原子模型を踏まえて、ラザフォードという物理学者が、1911年についに実験により今の原子核のモデルに辿り着いた。

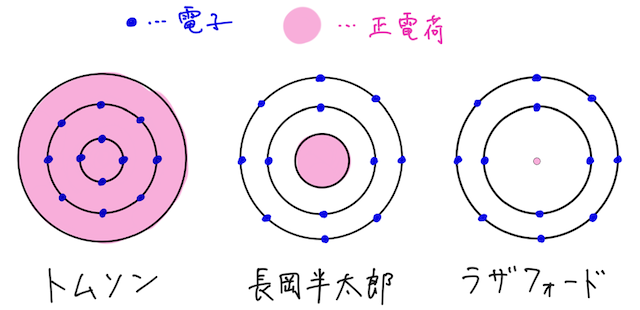
しかしながら、ラザフォードの原子模型に従うと、原子核の周りを回る電子は電磁波を出し、エネルギーを失うため、電子の軌道半径は小さくなってしまい安定した原子を表せない、という欠点があった。

ボーア模型

ラザフォードの原子模型をもとに、デンマークの物理学者であるボーアはいくつかの仮説を設定し、水素原子のスペクトルの式を導くことに成功した。

かなりすごいことをしているので、じっくりと見ていこう（水素原子のスペクトルの式の導出自体は、「エネルギー準位」という用語に続きます）。

ボーアがおいた仮説は大きく 「量子条件」 と 「振動数条件」 に分けられる。

量子条件

原子には、定常状態と呼ばれる軌道が複数存在し、この定常状態では電子は電磁波を放出することなく運動することができるとする。

電子の質量を 、速さを 、軌道の半径を 、とすると、定常状態は次の式で与えられる。（最後に補足あり）

ただし、 はプランク定数、 は自然数（）である。 がとびとびとなるので、定常状態の も もとびとびになる点に注意しておこう。

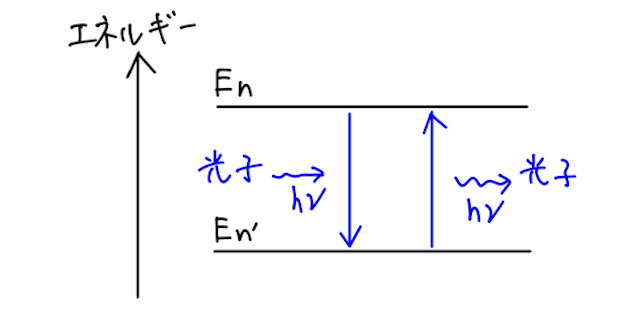
振動数条件

上の量子条件で見たように、定常状態の も もとびとびになるので、電子のエネルギーも によってとびとびの値となる。これをエネルギー準位と呼び、 と表すことにする。

このとき、電子がエネルギー準位 から、 とは別の に対応するエネルギー準位 に移るとき、1個の光子として吸収または放出する。

は光子の振動数であり、右辺は光子のエネルギーを表す点に着目しよう。

• のときは光子を放出
• のときは光子を吸収

となる。

ボーア半径

上の量子条件を用いると、水素原子内の電子がとりうる定常状態の軌道半径が求められる。

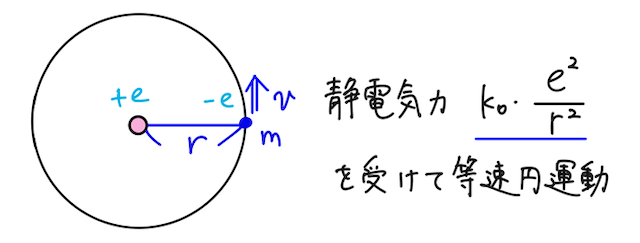
水素原子において、電気量 の原子核の周りを回る電子の質量を 、速さを 、軌道の半径を 、とすると、電子は静電気力を受けて等速円運動するので、電子の運動方程式は

と表せる（ はクーロンの法則の真空中での比例定数）。

定常状態の 式より

なので、これを使って 式の を消去して、 について整理すると、

となって、水素原子内の電子がとりうる定常状態の軌道半径が求められた。

この式によって求められる軌道半径をボーア半径という。

この半径と振動数条件を用いると、水素原子のスペクトルの式が求められる。詳しい導出は、「エネルギー準位」の用語にて。

補足

定常状態の式

が唐突すぎるわ！と突っ込みたい人も多いと思うので、ド・ブロイ波の式 を用いて、理解しやすい式にしてみよう。

ド・ブロイ波長の式

を用いて、 式を変形すると

となる。

この式を眺めると、電子の軌道の1周分の長さ（左辺）が、波長の整数倍（右辺）となるとき、定常状態を表すことになる。

これはすごく直感的で、確かに軌道の長さが波長の整数倍でなければ、波が干渉しあってそのような軌道は存在しないはず。

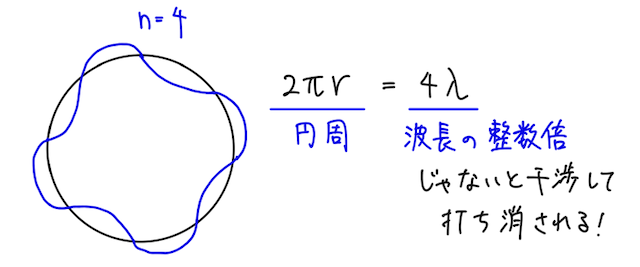
めっちゃ細かいことを言うと、ド・ブロイ波は、ボーアが理論を提唱してそれをもとに10年後くらいに提唱された概念なので、時系列的にはあとの話なのだが、テストでは、この 式を直感的に押さえておいて、それとド・ブロイ波長の式から量子条件の式を思い出すのがオススメ。