概要
事象 が起こったとして、そのもとで事象 の起こる確率を、 が起こったときの の条件つき確率といい、 で表し、次の式で計算できる。
つまり、 事象 と事象 がともに起こる場合の数を、 事象 が起こる場合の数で割る( は共通部分)。
この式の右辺の分母分子をそれぞれ、起こりうる全ての事象の場合の数で割ると、
となり、 のように場合の数を使って求めるのではなくて、事象 と事象 がともに起こる確率を、事象 が起こる確率で割っても計算できることがわかる。
例
言葉で書いても、ちょっと何言ってるかわからないので、例で考えよう。
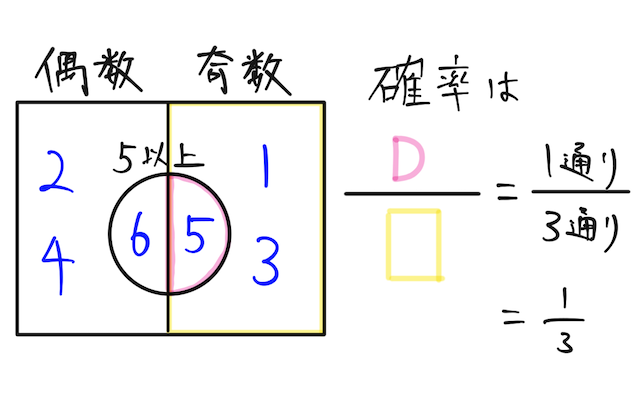
サイコロを 回振って、奇数が出たということがわかったとして、そのもとで目が 以上になっている確率は、
と計算できる。(奇数かつ 以上の目は 通り、奇数の目は 通りより)
イメージはこんな感じ。ベン図で捉えるとわかりやすい。
補足
上の例で、分母を全事象の 通りにしてしまうと、条件付き確率が求められない。
上の条件付き確率の式を変形した次の式を、かっこよく乗法定理と呼んだりする。
この式は、くじの例で考えるとわかりやすくい。 本中 本が当たりのくじから、 くんと さんが元に戻さずに順に引くとき、 と がともに当たる確率を考える。
が当たる確率を 、 が当たって が当たる条件付き確率を として、ともに当たる確率 は、
と求められる。無意識に使っている人が多いと思うが、一度意識して考えてみよう。






