事象
概要
難しいことはいいから、イメージを知りたい！と言う人は、サイコロを投げたりカードを引いたりしたときに起こる「出来事」を集めたもの だと思っておけば大丈夫。
詳しく知りたい人は、 試行によって起こりうる結果を集めた集合 のことだと理解しよう。集合なので、事象を考える時にはベン図 が使える。
例
たとえば、1つのサイコロを投げた時に、起こりうる結果の全体を
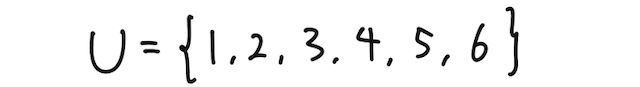
とする（ここでは、例えば1が出ることを1と表している）と、
■ 目が奇数になる事象は、下で3通り（つまり、集合の要素が3個あることに対応）
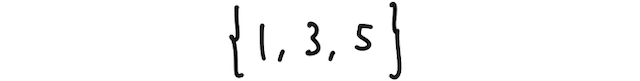
■ 目が5以上になる事象は、下で2通り（つまり、集合の要素が2個あることに対応）
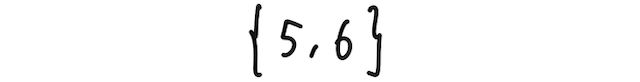
などの言い方ができる。
補足
余事象というのは、「そうじゃない事象」のこと。事象を集合として理解しておくと、余事象が、補集合に相当することもわかる。
ちなみに、試行とかいう言葉もあり、とてもややこしいが、 試行を行った結果が事象である、と頭を整理しておくと便利。
また、少し難しい言葉の話になってしまうが、起こりうる結果の全体を、上の例のように集合
例で考えると、さいころを1個投げたとき、全事象を
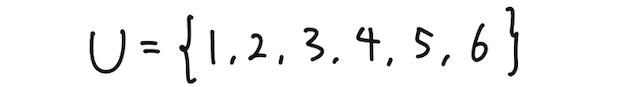
とする（ここでは、例えば1が出ることを1と表している）と、根元事象は
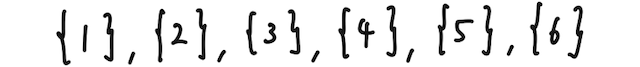
で6個ある。
一方で、全事象を
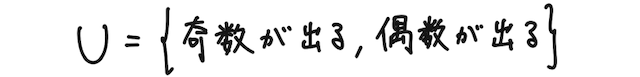
としてもよく、この場合の根元事象は
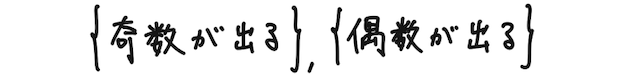
で2個となる。このように、全事象の決め方によって根元事象は変わってくる。
確率を考える上では、全ての根元事象が同じ確率で起こる（同様に確からしい） ことがとても大事になるので、頭の片隅に置いておこう。ここらへんの知識やコツを、動画でしっかり学びたい方は、ガチでノビる受験数学さんの確率シリーズがオススメ。