重心
概要
三角形の頂点から相対する辺の中点に対して下ろした線分のことを中線という。
三角形の
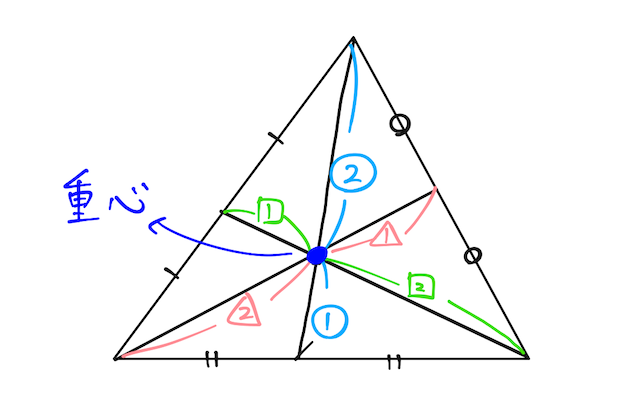
例
下図の点
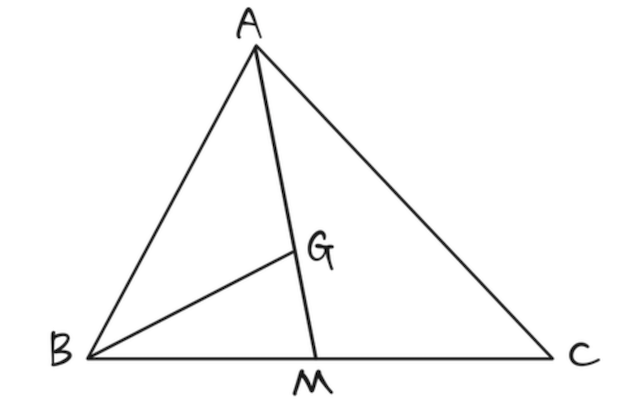
さらに、
と求められる。
証明
三角形の
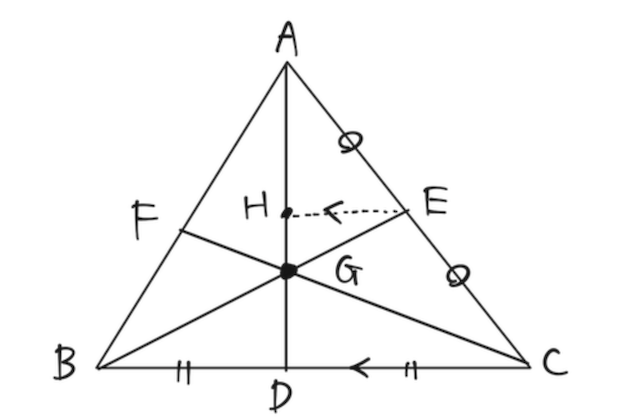
いま、重心の定義から
なので、代入して
が成り立つ。ここで平行線と線分比の性質から
が示される。他の中線の線分比についても同様に示される。
メネラウスの定理を使っても示せるので、興味のある方はやってみよう!わからない方は、AKITOさんの動画を見てみよう。
この用語を含むファイル
関連動画
三角形の頂点から相対する辺の中点に対して下ろした線分のことを中線という。
三角形の

下図の点

さらに、
と求められる。
三角形の

いま、重心の定義から
なので、代入して
が成り立つ。ここで平行線と線分比の性質から
が示される。他の中線の線分比についても同様に示される。
メネラウスの定理を使っても示せるので、興味のある方はやってみよう!わからない方は、AKITOさんの動画を見てみよう。
この用語を含むファイル
関連動画