中線定理
概要
どんな三角形
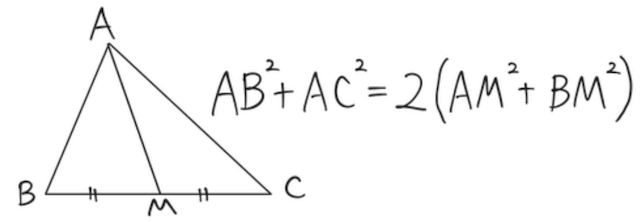
これを中線定理という。
証明
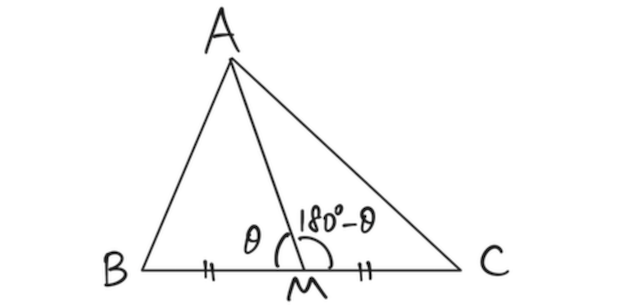
ここで、以下の式
が成り立つので(2つ目は180°関係の辞書を参照)、
と表される。よって、
となる。
補足
どの辺を足すかや
なお、実は中点じゃないバージョンに拡張したスチュワートの定理というものもあるので、興味のある方はMathkaratさんの動画を参照!
関連動画
どんな三角形
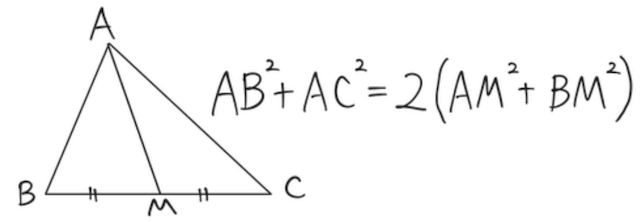
これを中線定理という。

ここで、以下の式
が成り立つので(2つ目は180°関係の辞書を参照)、
と表される。よって、
となる。
どの辺を足すかや
なお、実は中点じゃないバージョンに拡張したスチュワートの定理というものもあるので、興味のある方はMathkaratさんの動画を参照!
関連動画