内心

概要

三角形の頂点の内角の二等分線は 本あるが、その 本の直線は 点で交わり、その交点を内心という。

また、内心を中心として、三角形の全ての辺に内接する円を描くことができ、その円を内接円と呼ぶ。

内心に関する問題は、 角の二等分線の性質を使って考える問題が多い。

内心って何だっけ？と思ったら、 「角二（角煮）が苦手で内心ヒヤヒヤ」 で思い出せる。シチュエーションはご想像にお任せ。

例

について、、、 とする。内心を として、 と の交点を とする。 を求めよ。 を求めよ。

は内心なので、 は の二等分線。よって、角の二等分線の性質から

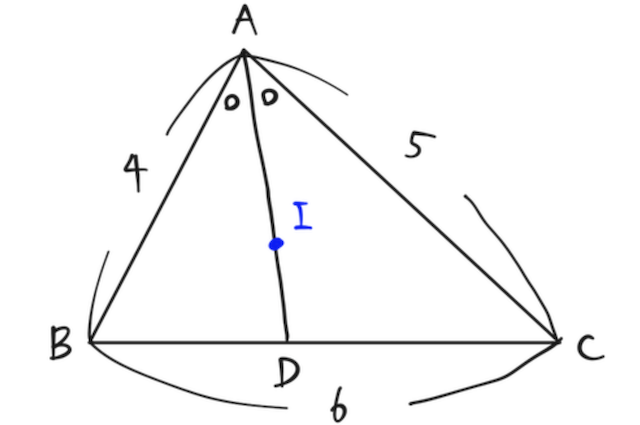
と求められる。

より、 の長さを求めることができ、

となる。 は内心なので、 は の二等分線。

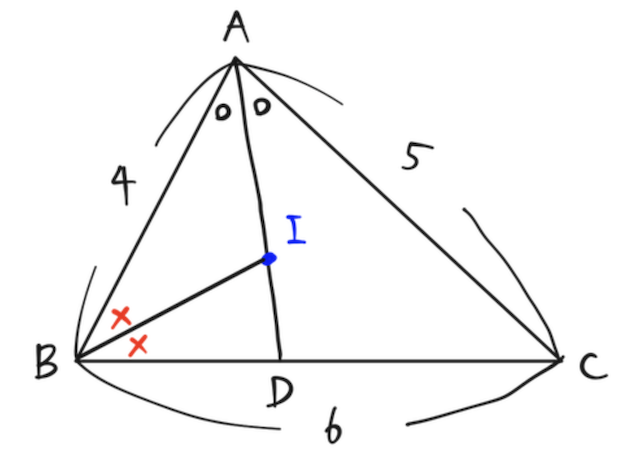
よって、角の二等分線の性質から

と求められる。

証明

内心が存在することについての証明は例えば古賀真輝さんの動画や、AKITOさんの動画を参照。