概要
曲線 、 が で接するための必要十分条件 (つまり全く同じ条件)は、
が成立すること。日本語にすると、 曲線が において同じ値となり(これが つ目の式に相当)、 同じ接線の傾き(微分係数) を持つ(これが つ目の式に相当)ということ。下のイメージで理解しておけばわざわざ覚えなくて済む。
片方だけではダメで、例えば で同じ値を取るけど微分係数が違う場合は、 曲線がクロスしてしまうし、
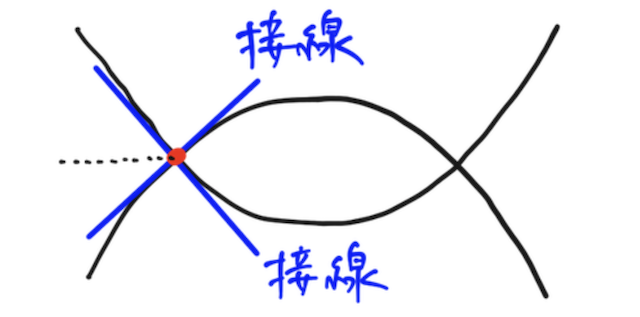
同じ微分係数だけど、違う値を取る場合は、 曲線が離れてしまう。
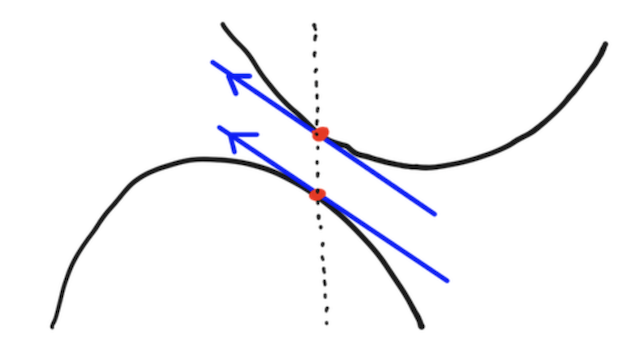
なので、どっちもそろって初めて「曲線が接する」と言える。
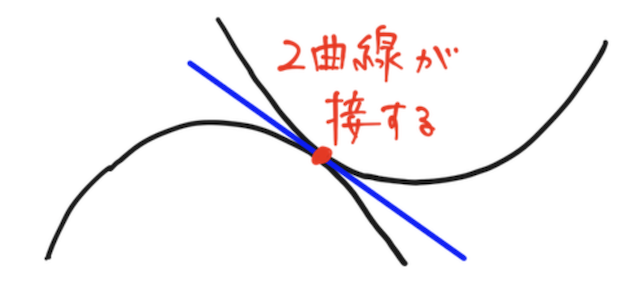
下の、 重解を使った考え方との頭の整理も大事。
<重解を使った考え方>
もし 曲線 、 が整式(イメージは 次関数や 次関数のような多項式)だった場合、接するための必要十分条件は、
と書くこともでき、こっちで考えた方が考えやすいこともある(ただこれは 次関数や 次関数のような整式じゃないと使えないので、注意が必要)。出てきた重解が接点の 座標となる。また、 が 次関数だったら 「判別式 」 でいける。
例
つの放物線
が接するとき、定数 の値を求める。
上の考え方でいくと、接点の 座標を とおくと、接するための必要十分条件は、
つまり、
となる。ここで、それぞれの導関数が
となることを用いた。
①②より を消去すると、
と求められる。このとき も存在する。
もう一つ、重解を使った解き方だと、
を考えて、これが重解を持つための必要十分条件は
と同じ解が求まる。
補足
「共通接線」という言葉との違いも大事。共通接線は、 曲線に対してどっちにも接する接線のことなので、図の通り 曲線が共有点を持つ必要はない。
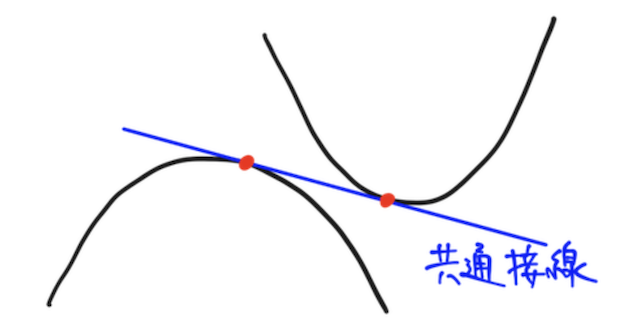
ちなみに、曲線と書いてるが、直線でもOK。(直線の場合は、わざわさこういう条件を立てなくても解けることも多々ある)
「 曲線が接する」と言われたら、接点の 座標を置いてしまって、この 本の式を立てれば数式にできるので、 絶大な安心感はあるが、しっかり考えて上のように頭を整理しないと、頭がごちゃごちゃになって解きたくなくなるテーマでもある。










