階差数列
概要
数列
ただ、項の差を計算すると、
と規則的になっていそう。そこで階差数列が登場する。
数列
階差数列を新しく
つまり、イメージは下の通り。
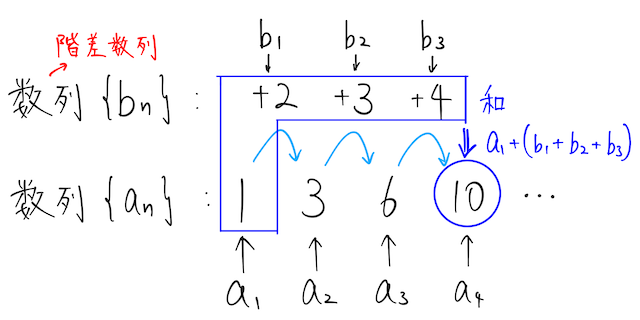
注意しないといけないのは、この一般項の式は
なぜ
例
上の例で考えると、
と求められる(
一方、
に
よってまとめることができて、
となる。
補足
上の例のように、シグマの中に書く、階差数列
漸化式で、
という形にピンときたら、それは階差数列を使って一般項を計算できる。
関連動画
数列
ただ、項の差を計算すると、
と規則的になっていそう。そこで階差数列が登場する。
数列
階差数列を新しく
つまり、イメージは下の通り。

注意しないといけないのは、この一般項の式は
なぜ
上の例で考えると、
と求められる(
一方、
に
よってまとめることができて、
となる。
上の例のように、シグマの中に書く、階差数列
漸化式で、
という形にピンときたら、それは階差数列を使って一般項を計算できる。
関連動画