等差数列

概要

という数の並びをイメージしよう。ずつ増えていることがわかる。

このように、 次の数との差が常に等しい数列を、「等差数列」 と呼ぶ。（数列とカッコよく書いているが、簡単に言うと数の並び）

また、次の数との差を公差と呼び、基本的に で表す。この例では 。

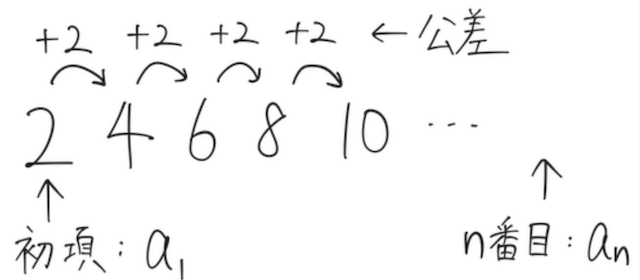
数列の何番目にどういう数字がくるか、すぐにわかるようにしたものが、「一般項」と言われるもので、第 項目の数を を使って表現し、基本的に と書く。

等差数列の場合は、

となる。（ は初項と呼ばれ、つまり数列の最初の数を表す。この例では ）

これは、最初の数に、公差を 個足したものが、 番目の数になると考えると理解できる。

この式によって、 数列の何番目にどういう数字がくるか、すぐに計算できる。たとえば、 番目にくる数は、

とわかる。

等差数列の「和」 についても知っておこう。等差数列の初項から第 項までの和（つまり ）は、

で計算できる。（和は基本的に を使う）

たとえば、上の数列の初項から第 項までの和を計算すると、まず一般項の式から

なので、

とわかる。

証明

足す順序を入れ替えると、

とも書ける。ここで、 と を辺々足すと、

となる。

補足

• 難しそうな漢字がたくさん出てくるが、 簡単な数の並びとイメージで考えるようにすると、一気に数列と仲良くなれる。
• 和については、 から足さなくてもOK。その場合は 項数を使う。例えば第 項から第 項までの和は、項数の を使って、下の式で計算できる。

• 漸化式で、 という形にピンときたら、それは等差数列を表している。