線分の通過領域〜〜2014東大〜〜

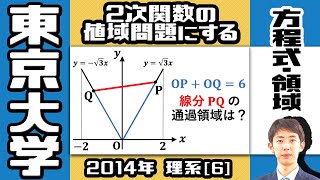
＜問題＞ 座標平面の原点をOで表す. 線分y=√3x(0≦x≦2)上の点Pと， 線分y=−√3x(−2≦x≦0)上の点Qが， 線分OPと線分OQの長さの和が6となるように動く. このとき，線分PQの通過する領域をDとする. (1)sを0≦s≦2を満たす実数とするとき，点(s,t)がDに入るような t の範囲を求めよ. (2)Dを図示せよ． ＜ソース＞ 2014 東大 (2)がメインです． (1)は「ファクシミリ論法で解け」という指示ですね． わざわざこれがあるということは，「包絡線を使うな」ということでしょうかね〜． ＜関連問題＞ 前回↓【京大】線分の通過領域 https://youtu.be/hROdMsjWFu4 ＜はやくち解説とは＞ かったるい説明に嫌気がさしたときに見る動画。早口×早送りで解説しました。雰囲気を掴んでもらえたらいいと思っています。 #東大数学